CTF of Z2BNS
0%

回文数

发表于 更新于 分类于 ，
| 阅读次数： |
Valine：
本文字数： 1.6k 阅读时长 ≈ 1 分钟

题目地址

难度：⭐

题目描述：

判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

示例1：

1
2
输入：121
输出：true

示例2：

1
2
3
输入：-121
输出：false
解释：从左向右读，为-121。从右向左读，为121-。因此它不是一个回文数。

示例3：

1
2
3
输入：10
输出：false
解释：从右向左读，为01。因此它不是一个回文数。

进阶：

你能不将整数转为字符串来解决这个问题吗？

🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️解题过程🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️
解题过程：

思路：

进阶说不要转成字符串能解决吗，我本来就没打算把整数转成字符串🤣，这题跟上次做的那道整数反转采用相似的想法，把这个整数反转得到的值和原来的整数进行比较，若相等则是回文数，否则则输出false。

下面是自己提交通过的代码，执行用时12ms，内存消耗6.1M：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    bool isPalindrome(int x) {
        //x为负数时绝对不是回文数
        if(x<0){
            return false;
        }
        int rev=0;
        int tmp=x;
        //反转
        while(x!=0){
            int pop=x%10;
            x/=10;
            //要把所有合理的输入所产生的情况都考虑到，以前在其它平台做的题还是不严谨
            //提前判定反转后是否溢出
            if(rev>INT_MAX/10 || (rev==INT_MAX/10 &&pop>7))return false;
            if(rev<INT_MIN/10 || (rev==INT_MIN/10 && pop<-8)) return false;
            rev=rev*10+pop; 
        }
        if(rev==tmp){
            return true;
        }else{
            return false;
        }
    }
};

不过既然还可以整数转字符串来做，就实现了吧，下面是代码，执行用时20ms，内存消耗6.1M：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool isPalindrome(int x) {
        //整数x转成字符串
        string s= to_string(x);
        int len=s.length();
        //字符串前后进行比较
        for(int i=0;i<len/2;i++){
            //c++没有后面开始的索引，不然还可以用s[-i-1]
            if(s[i]!=s[len-i-1]){
                return false;
            }
        }
        return true;
    }
};
💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎官 方 题 解💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎
官方题解：

方法：反转一半数字
思路

映入脑海的第一个想法是将数字转换为字符串，并检查字符串是否为回文。但是，这需要额外的非常量空间来创建问题描述中所不允许的字符串。

第二个想法是将数字本身反转，然后将反转后的数字与原始数字进行比较，如果它们是相同的，那么这个数字就是回文。
但是，如果反转后的数字大于 $\text{int.MAX}$，我们将遇到整数溢出问题。

按照第二个想法，为了避免数字反转可能导致的溢出问题，为什么不考虑只反转 $\text{int}$ 数字的一半？毕竟，如果该数字是回文，其后半部分反转后应该与原始数字的前半部分相同。

例如，输入 1221，我们可以将数字 “1221” 的后半部分从 “21” 反转为 “12”，并将其与前半部分 “12” 进行比较，因为二者相同，我们得知数字 1221 是回文。

算法

首先，我们应该处理一些临界情况。所有负数都不可能是回文，例如：-123 不是回文，因为 - 不等于 3。所以我们可以对所有负数返回 false。除了 0 以外，所有个位是 0 的数字不可能是回文，因为最高位不等于 0。所以我们可以对所有大于 0 且个位是 0 的数字返回 false。

现在，让我们来考虑如何反转后半部分的数字。

对于数字 1221，如果执行 1221 % 10，我们将得到最后一位数字 1，要得到倒数第二位数字，我们可以先通过除以 10 把最后一位数字从 1221 中移除，1221 / 10 = 122，再求出上一步结果除以 10 的余数，122 % 10 = 2，就可以得到倒数第二位数字。如果我们把最后一位数字乘以 10，再加上倒数第二位数字，1 * 10 + 2 = 12，就得到了我们想要的反转后的数字。如果继续这个过程，我们将得到更多位数的反转数字。

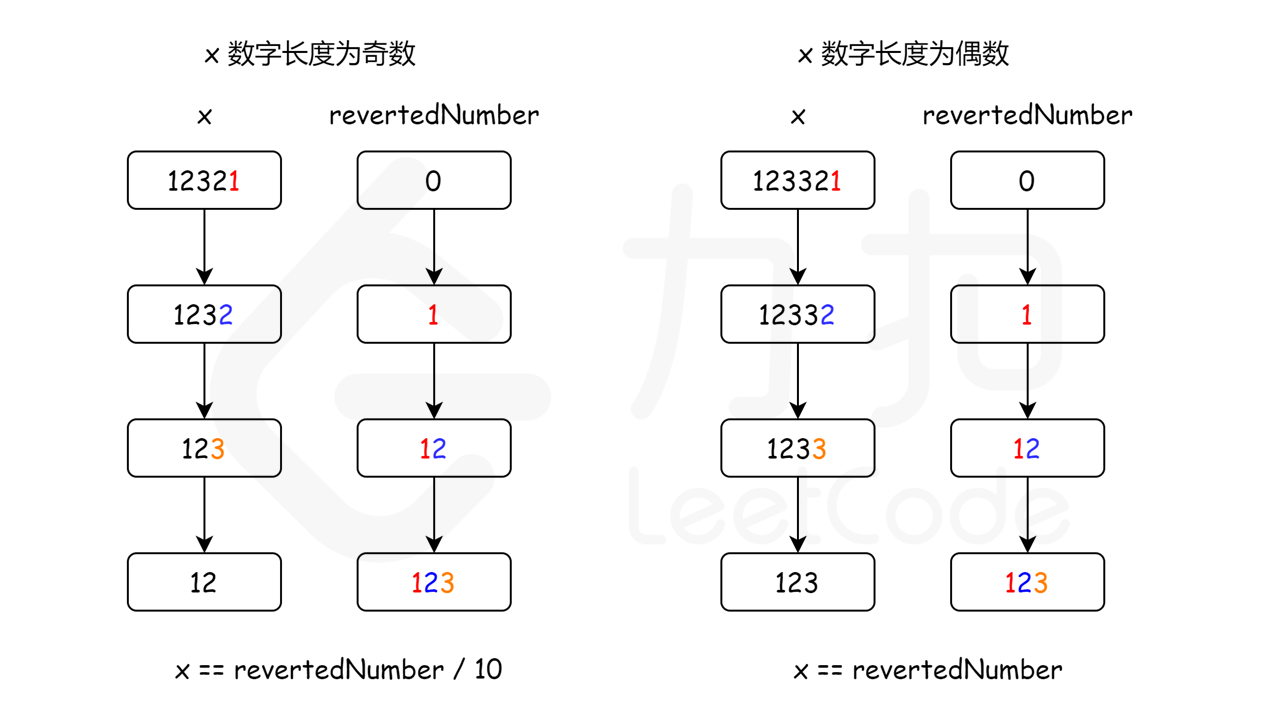
现在的问题是，我们如何知道反转数字的位数已经达到原始数字位数的一半？

由于整个过程我们不断将原始数字除以 10，然后给反转后的数字乘上 10，所以，当原始数字小于或等于反转后的数字时，就意味着我们已经处理了一半位数的数字了。

img

代码（执行用时16ms，内存消耗6M）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    bool isPalindrome(int x) {
        // 特殊情况：
        // 如上所述，当 x < 0 时，x 不是回文数。
        // 同样地，如果数字的最后一位是 0，为了使该数字为回文，
        // 则其第一位数字也应该是 0
        // 只有 0 满足这一属性
        if (x < 0 || (x % 10 == 0 && x != 0)) {
            return false;
        }

        int revertedNumber = 0;
        while (x > revertedNumber) {
            revertedNumber = revertedNumber * 10 + x % 10;
            x /= 10;
        }

        // 当数字长度为奇数时，我们可以通过 revertedNumber/10 去除处于中位的数字。
        // 例如，当输入为 12321 时，在 while 循环的末尾我们可以得到 x = 12，revertedNumber = 123，
        // 由于处于中位的数字不影响回文（它总是与自己相等），所以我们可以简单地将其去除。
        return x == revertedNumber || x == revertedNumber / 10;
    }
};

复杂度分析

  • 时间复杂度：$O(log(n))$，对于每次迭代，我们会将输入除以10，因此时间复杂度为O(log(n))。
  • 空间复杂度：$O(1)$。我们只需要常数空间存放若干变量。
⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳总 结⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳
总结：

感觉自己写的已经差不多是最优了，但题解总是能进一步对算法优化，反转一半数字并用反转的前半部分和反转的后半部分比较作为反转完成条件，这个方法就很nice。我觉得自己缺乏算法锻炼、性能优化这方面的思维。很多时候就觉得只要完成功能就ok了，对性能这方面没有太大的考虑，其实这方面还是挺重要的。还是需要做多些题，不断地学习进步吧🤓。

------------- THE END! THANKS! -------------