CTF of Z2BNS
0%

有效的山脉数组

发表于 更新于 分类于 ，
| 阅读次数： |
Valine：
本文字数： 980 阅读时长 ≈ 1 分钟

题目地址

题目名称：有效的山脉数组

难度：⭐

题目描述：

给定一个数组A，如果它是有效的山脉数组就返回true，否则返回false。

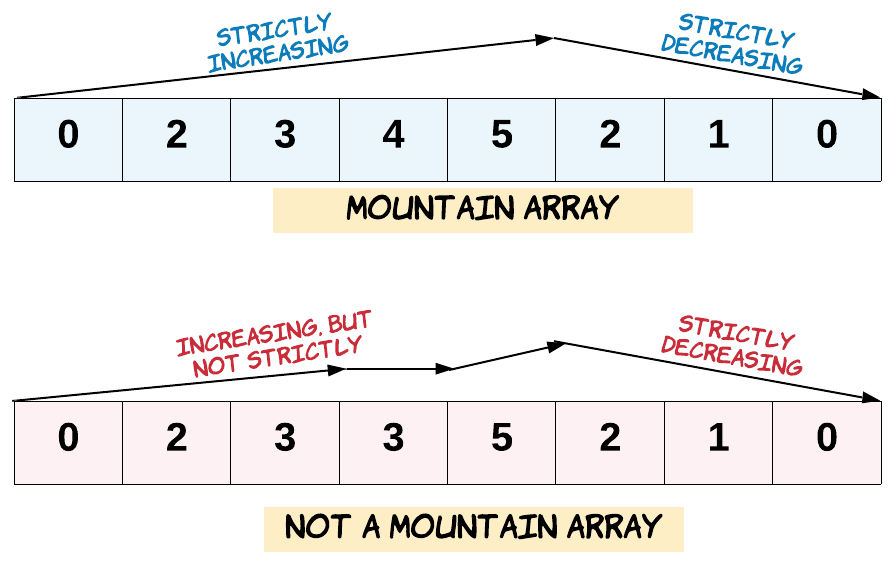
让我们回顾一下，如果A满足下述条件，那么它是一个山脉数组：

  • A.length >= 3

  • 在 0 < i < A.length - 1 条件下，存在 i 使得：

    • A[0] < A[1] < ... A[i-1] < A[i]
  • A[i] > A[i+1] > ... > A[A.length - 1]

img

示例1：

1
2
输入：[2,1]
输出：false

示例2：

1
2
输入：[3,5,5]
输出：false

示例3：

1
2
输入：[0,3,2,1]
输出：true

提示：

  1. 0 <= A.length <= 10000
  2. 0 <= A[i] <= 10000
🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️解题过程🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️
解题过程：

思路：

可以两次for循环每次循环到中间最大值，第一次从前往后遍历升序判断，第二次从后往前遍历升序判断。

c++代码：(执行用时56ms，击败90.92%，内存消耗21.2M，击败5.27%)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    bool validMountainArray(vector<int>& A) {
        bool result = false;
        if(A.size()<3){
            return false;
        }
        int i;
        for(i = 0; i < A.size() - 1; ++i) {
            //前半部分结束
            if(A[i] >= A[i + 1]) {
                if(i == 0) {
                    result = false;
                } else {
                    //前半部分满足
                    result = true;
                }
                break;
            }
        }
        //判断后半部分
        for(int j = i; j < A.size() - 1; ++j) {
            //不是山脉数组
            if(A[j] <= A[j + 1]) {
                result = false;
            }
        }
        return result;
    }
};
💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎官 方 题 解💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎
官方题解：

方法一：线性扫描

按题意模拟即可。我们从数组的最左侧开始向右扫描，直到找到第一个不满足 $A[i] < A[i + 1]$ 的下标$i$，那么 $i$ 就是这个数组的最高点的下标。如果 $i = 0$ 或者不存在这样的 $i$（即整个数组都是单调递增的），那么就返回 $false$。否则从 $i$ 开始继续向右扫描，判断接下来的的下标 $j$ 是否都满足 $A[j] > A[j + 1]$，若都满足就返回 $true$，否则返回 $false$。

代码（执行用时60ms，击败81.85%，内存21.1M，击败5.27%）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    bool validMountainArray(vector<int>& A) {
        int N = A.size();
        int i = 0;

        // 递增扫描
        while (i + 1 < N && A[i] < A[i + 1]) {
            i++;
        }

        // 最高点不能是数组的第一个位置或最后一个位置
        if (i == 0 || i == N - 1) {
            return false;
        }

        // 递减扫描
        while (i + 1 < N && A[i] > A[i + 1]) {
            i++;
        }

        return i == N - 1;
    }
};

复杂度分析

  • 时间复杂度：$O(N)$，其中 $N$ 是数组 $A$ 的长度。
  • 空间复杂度：$O(1)$。
⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳总 结⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳
总结：

我的解题思路和官方题解是一样的，只不过官方题解代码可能更简洁清楚一些。感觉官方题解挺好的啊，为什么效率还没我的高呢😅

------------- THE END! THANKS! -------------