CTF of Z2BNS
0%

汉明距离

发表于 更新于 分类于 ，
| 阅读次数： |
Valine：
本文字数： 1.8k 阅读时长 ≈ 2 分钟

题目地址

难度：⭐

题目描述：

两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

给出两个整数 x 和 y，计算它们之间的汉明距离。

示例：

1
2
3
4
5
6
7
8
9
10
输入: x = 1, y = 4

输出: 2

解释:
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑

上面的箭头指出了对应二进制位不同的位置。

注意：

  • 0 ≤ x, y < $2^{31}$​.
🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️解题过程🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️
解题过程：

思路：

其实就是两个整数异或运算，得到的结果二进制位相加就是汉明距离。

c++代码：(执行用时4ms，击败26.92%，内存消耗6.3M，击败5.02%）

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int hammingDistance(int x, int y) {
        int result=0;
        //也就是求两个数字异或结果的二进制各位相加
        int tmp=x^y;
        while(tmp){
            result+=tmp%2;
            tmp/=2;
        }
        return result;
    }
};
💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎官 方 题 解💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎
官方题解:

思路
汉明距离广泛应用于多个领域。在编码理论中用于错误检测，在信息论中量化字符串之间的差异。

两个整数之间的汉明距离是对应位置上数字不同的位数。

根据以上定义，提出一种 XOR 的位运算，当且仅当输入位不同时输出为 1。

img

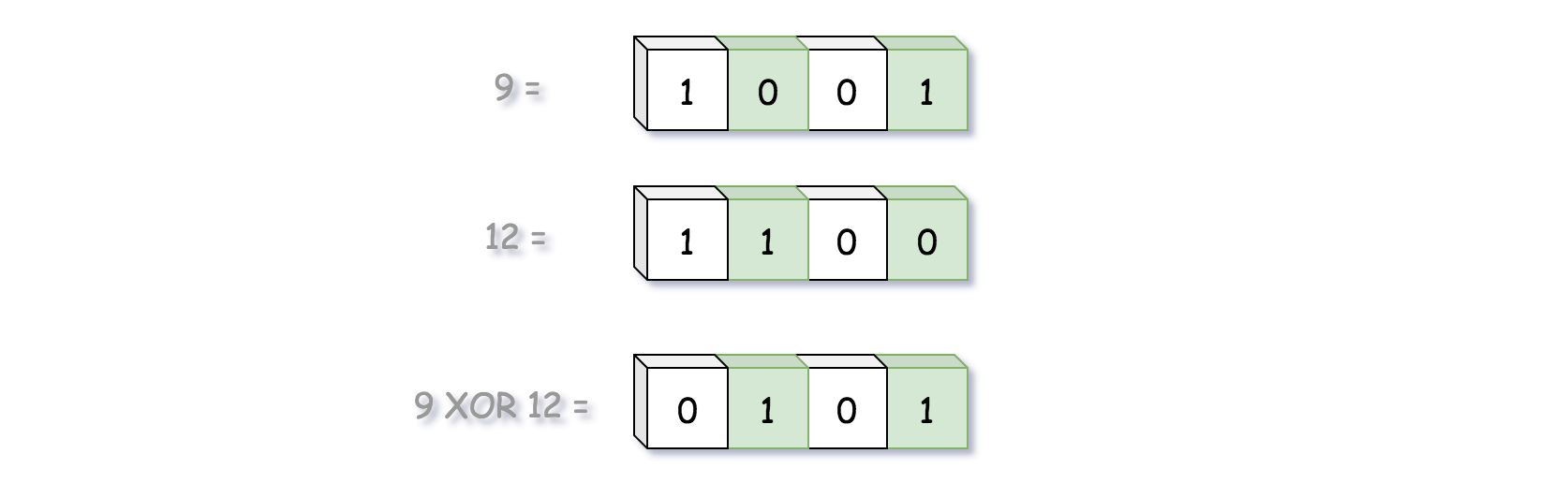
计算 x 和 y 之间的汉明距离，可以先计算 x XOR y，然后统计结果中等于 1 的位数。

现在，原始问题转换为位计数问题。位计数有多种思路，将在下面的方法中介绍。

方法一：内置位计数功能

思路

大多数编程语言中，都存在各种内置计算等于 1 的位数函数。如果这是一个项目中的问题，应该直接使用内置函数，而不是重复造轮子。

但这是一个力扣问题，有人会认为使用内置函数就好像使用 使用 LinkedList 实现 LinkedList。对此，我们完全赞同。因此后面会有手工实现的位计数算法。

python代码：

1
2
3
class Solution:
    def hammingDistance(self, x: int, y: int) -> int:
        return bin(x ^ y).count('1')

复杂度分析

  • 时间复杂度：$O(1)$。

  • 该算法有两个操作。计算 XOR 花费恒定时间。

  • 调用内置的 bitCount 函数。最坏情况下，该函数复杂度为$O(k)$，其中 $k$ 是整数的位数。在 Python 和 Java 中 Integer 是固定长度的。因此该算法复杂度恒定，与输入大小无关。

  • 空间复杂度：$O(1)$，使用恒定大小的空间保存 XOR 的结果。

    • 假设内置函数也使用恒定空间。

方法二：移位

思路

为了计算等于 1 的位数，可以将每个位移动到最左侧或最右侧，然后检查该位是否为 1。

更准确的说，应该进行逻辑移位，移入零替换丢弃的位。

img

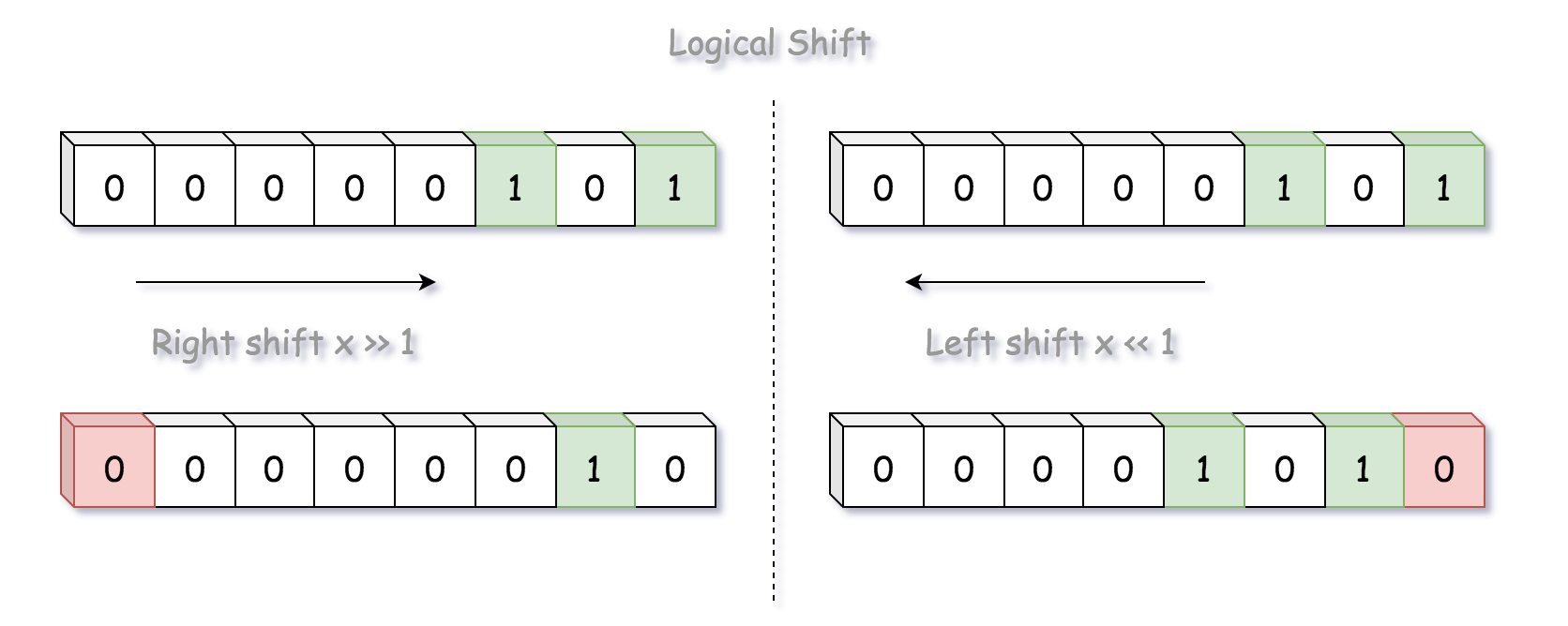
这里采用右移位，每个位置都会被移动到最右边。移位后检查最右位的位是否为 1 即可。检查最右位是否为 1，可以使用取模运算（i % 2）或者 AND 操作（i & 1），这两个操作都会屏蔽最右位以外的其他位。

python代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution(object):
    def hammingDistance(self, x, y):
        """
        :type x: int
        :type y: int
        :rtype: int
        """
        xor = x ^ y
        distance = 0
        while xor:
            # mask out the rest bits
            if xor & 1:
                distance += 1
            xor = xor >> 1
        return distance

复杂度分析

  • 时间复杂度：$O(1)$，在 Python 和 Java 中 Integer 的大小是固定的，处理时间也是固定的。 32 位整数需要 32 次迭代。

  • 空间复杂度：$O(1)$，使用恒定大小的空间。

方法三：布赖恩·克尼根算法

思路

方法二是逐位移动，逐位比较边缘位置是否为 1。寻找一种更快的方法找出等于 1 的位数。

是否可以像人类直观的计数比特为 1 的位数，跳过两个 1 之间的 0。例如：10001000。

上面例子中，遇到最右边的 1 后，如果可以跳过中间的 0，直接跳到下一个 1，效率会高很多。

这是布赖恩·克尼根位计数算法的基本思想。该算法使用特定比特位和算术运算移除等于 1 的最右比特位。

当我们在 number 和 number-1 上做 AND 位运算时，原数字 number 的最右边等于 1 的比特会被移除。

img

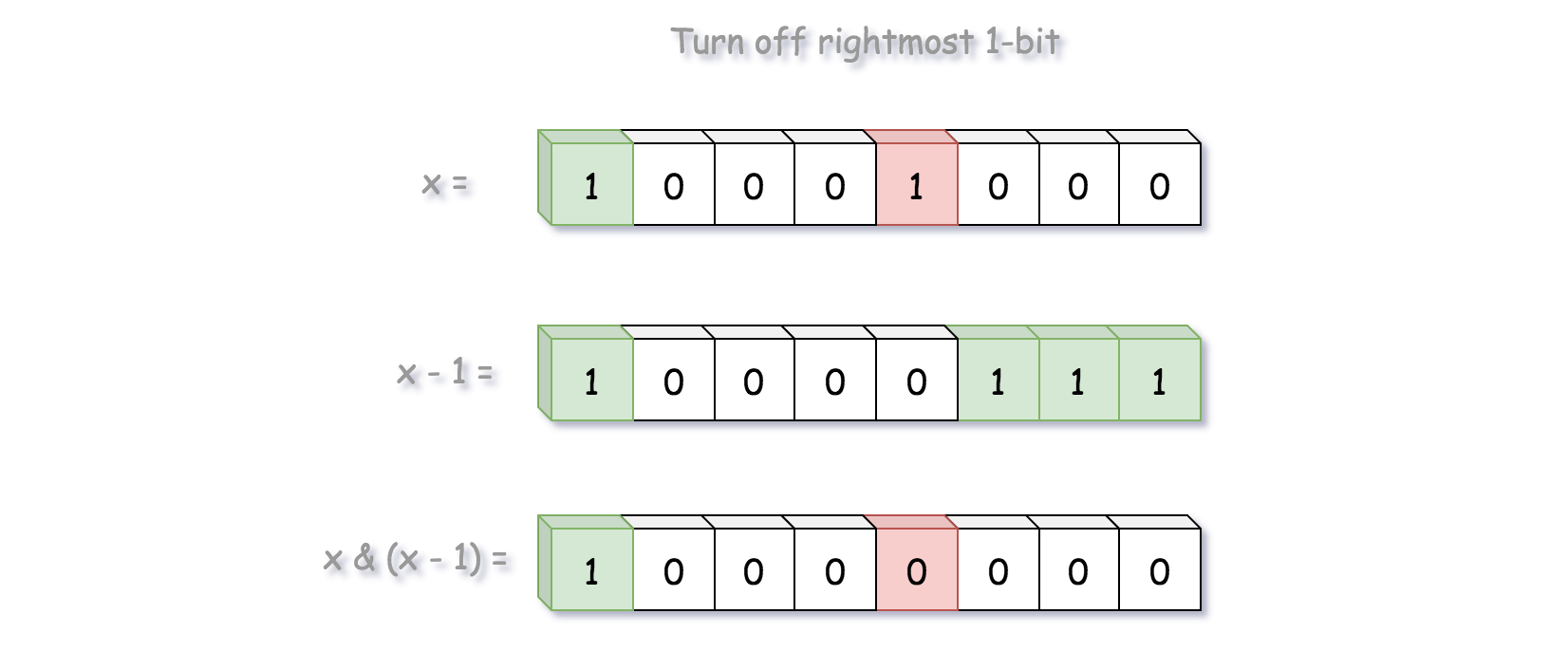
基于以上思路，通过 2 次迭代就可以知道 10001000 中 1 的位数，而不需要 8 次。

python代码：

1
2
3
4
5
6
7
8
9
class Solution:
    def hammingDistance(self, x, y):
        xor = x ^ y
        distance = 0
        while xor:
            distance += 1
            # remove the rightmost bit of '1'
            xor = xor & (xor - 1)
        return distance

注意：该算法发布在 1988 年 《C 语言编程第二版》的练习中（由 Brian W. Kernighan 和 Dennis M. Ritchie 编写），但是 Donald Knuth 在 2006 年 4 月 19 日指出，该方法第一次是由 Peter Wegner 在 1960 年的 CACM3 上出版。顺便说一句，可以在上述书籍中找到更多位操作的技巧。

复杂度分析

  • 时间复杂度：$O(1)$。

    • 与移位方法相似，由于整数的位数恒定，因此具有恒定的时间复杂度。
  • 但是该方法需要的迭代操作更少。
  • 空间复杂度：$O(1)$，与输入无关，使用恒定大小的空间。
⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳总 结⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳
总结：

官方题解怎么都是python或者java代码，虽然python和java我都会，但是我现在在学c++，还是全部用c++实现吧，可以借鉴官方题解的算法思想😗

------------- THE END! THANKS! -------------