CTF of Z2BNS
0%

矩阵对角线元素的和

发表于 更新于 分类于 ，
| 阅读次数： |
Valine：
本文字数： 911 阅读时长 ≈ 1 分钟

题目地址

难度：⭐

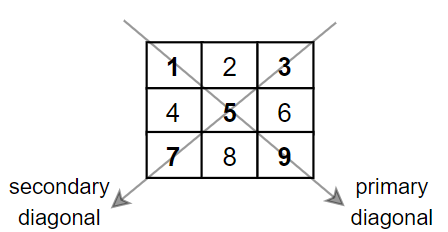
题目描述：

给你一个正方形矩阵 mat，请你返回矩阵对角线元素的和。

请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。

示例1：

img

1
2
3
4
5
6
输入：mat = [[1,2,3],
            [4,5,6],
            [7,8,9]]
输出：25
解释：对角线的和为：1 + 5 + 9 + 3 + 7 = 25
请注意，元素 mat[1][1] = 5 只会被计算一次。

示例2：

1
2
3
4
5
输入：mat = [[1,1,1,1],
            [1,1,1,1],
            [1,1,1,1],
            [1,1,1,1]]
输出：8

示例3：

1
2
输入：mat = [[5]]
输出：5

限制：

  • n == mat.length == mat[i].length
  • 1 <= n <= 100
  • 1 <= mat[i][j] <= 100
🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️解题过程🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️
解题过程：

思路：

根据题目描述模拟，直接加上对角线上的元素值，注意矩阵的行数为奇数时会重复加上主副对角线的重叠值，需要减去。

c++代码：(执行用时28ms，击败98.91%，内存消耗11.5M，击败5.03%）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int diagonalSum(vector<vector<int>>& mat) {
        int result=0;
        int n=mat.size();
        for(int i=0;i<n;++i){
            result+=mat[i][i];
            result+=mat[i][n-i-1];
        }
        //n是奇数，减去重复加上的中间的值
        if(n%2!=0){
            result-=mat[(n-1)/2][(n-1)/2];
        }
        return result;
    }
};
💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎官 方 题 解💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎
官方题解:

方法一：遍历矩阵
思路与算法

遍历整个矩阵，如果当前坐标 (i, j)(i,j) 满足 i = ji=j 或者 i + j = n - 1i+j=n−1，就把当前的数字加入到答案中。

c++代码：（执行32ms，击败93.54%，内存11.5M，击败5.16%）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int diagonalSum(vector<vector<int>>& mat) {
        int n = mat.size(), sum = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == j || i + j == n - 1) {
                    sum += mat[i][j];
                }
            }
        }
        return sum;
    }
};

复杂度分析

  • 时间复杂度：$O(n^2)$，其中 $n$是矩阵 $\textit{mat}$的边长。
  • 空间复杂度：$O(1)$。

方法二：逐行取数
思路与算法

逐行遍历，记当前的行号为 $i$，对于一行我们把 $(i, i)$ 位置和 加入答案。这样如果 $n$ 是奇数的话，最中间的格子会被加入两次。所以 $n$ 为奇数的时候，我们需要减掉矩阵最中心的那个值。

c++代码：（执行36ms，击败74.17%，内存11.5M，击败5.03%）

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int diagonalSum(vector<vector<int>>& mat) {
        int n = mat.size(), sum = 0, mid = n / 2;
        for (int i = 0; i < n; ++i) {
            sum += mat[i][i] + mat[i][n - 1 - i];
        }
        return sum - mat[mid][mid] * (n & 1);
    }
};

复杂度分析

  • 时间复杂度：，其中 $n$是矩阵 $\textit{mat}$ 的边长。
  • 空间复杂度：$O(1)$。
⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳总 结⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳
总结：

简单，没啥可说的，go on！🙄

------------- THE END! THANKS! -------------