CTF of Z2BNS
0%

距离顺序排列矩阵单元格

发表于 分类于 ，
| 阅读次数： |
Valine：
本文字数： 1.6k 阅读时长 ≈ 1 分钟

题目地址

难度：⭐

题目描述：

给出 R 行 C 列的矩阵，其中的单元格的整数坐标为 (r, c)，满足 0 <= r < R 且 0 <= c < C。

另外，我们在该矩阵中给出了一个坐标为 (r0, c0) 的单元格。

返回矩阵中的所有单元格的坐标，并按到 (r0, c0) 的距离从最小到最大的顺序排，其中，两单元格(r1, c1) 和 (r2, c2) 之间的距离是曼哈顿距离，|r1 - r2| + |c1 - c2|。（你可以按任何满足此条件的顺序返回答案。）

示例1：

1
2
3
输入：R = 1, C = 2, r0 = 0, c0 = 0
输出：[[0,0],[0,1]]
解释：从 (r0, c0) 到其他单元格的距离为：[0,1]

示例2：

1
2
3
4
输入：R = 2, C = 2, r0 = 0, c0 = 1
输出：[[0,1],[0,0],[1,1],[1,0]]
解释：从 (r0, c0) 到其他单元格的距离为：[0,1,1,2]
[[0,1],[1,1],[0,0],[1,0]] 也会被视作正确答案。

示例3：

1
2
3
4
输入：R = 2, C = 3, r0 = 1, c0 = 2
输出：[[1,2],[0,2],[1,1],[0,1],[1,0],[0,0]]
解释：从 (r0, c0) 到其他单元格的距离为：[0,1,1,2,2,3]
其他满足题目要求的答案也会被视为正确，例如 [[1,2],[1,1],[0,2],[1,0],[0,1],[0,0]]

提示：

  1. 1 <= R <= 100
  2. 1 <= C <= 100
  3. 0 <= r0 < R
  4. 0 <= c0 < C
🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️解题过程🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️
解题过程：

思路：

遍历矩阵，计算每个单元格与（r0，c0）的曼哈顿距离d，然后d作为键，单元格的坐标作为值存到multimap容器中，利用multimap容器的特性：容器中元素按关键字排序，并且允许多个关键字相同。遍历完成得到按曼哈顿距离升序排序的multimap容器，遍历multimap把值依次放到结果中，最后返回。

c++代码：(执行用时176ms，击败17.98%，内存消耗29M，击败15.48%）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<vector<int>> allCellsDistOrder(int R, int C, int r0, int c0) {
        vector<vector<int>> result;
        multimap<int,vector<int>> m;
        vector<int> v;
        int d;
        for(int i=0;i<R;++i){
            for(int j=0;j<C;++j){
                v.clear();
                v.emplace_back(i);
                v.emplace_back(j);
                d=abs(r0-i)+abs(c0-j);
                //map可以用m[d]=v赋值，multimap不能
                m.insert(pair<int,vector<int>>(d,v));
            }
        }
        for(auto tmp:m){
            result.emplace_back(tmp.second);
        }
        return result;
    }
};
💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎官 方 题 解💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎
官方题解:

方法一：直接排序

思路及解法

最容易想到的方法是首先存储矩阵内所有的点，然后将其按照哈曼顿距离直接排序。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    vector<vector<int>> allCellsDistOrder(int R, int C, int r0, int c0) {
        vector<vector<int>> ret;
        for (int i = 0; i < R; i++) {
            for (int j = 0; j < C; j++) {
                ret.push_back({i, j});
            }
        }
        sort(ret.begin(), ret.end(), [=](vector<int>& a, vector<int>& b) {
            return abs(a[0] - r0) + abs(a[1] - c0) < abs(b[0] - r0) + abs(b[1] - c0);
        });
        return ret;
    }
};

复杂度分析

  • 时间复杂度：$O(RC \log(RC))$，存储所有点时间复杂度 $O(RC)$，排序时间复杂度 $O(RC \log(RC))$。

  • 空间复杂度：$O(log(RC))$，即为排序需要使用的栈空间，不考虑返回值的空间占用。

方法二：桶排序

思路及解法

注意到方法一中排序的时间复杂度太高。实际在枚举所有点时，我们可以直接按照哈曼顿距离分桶。这样我们就可以实现线性的桶排序。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int dist(int r1, int c1, int r2, int c2) {
        return abs(r1 - r2) + abs(c1 - c2);
    }

    vector<vector<int>> allCellsDistOrder(int R, int C, int r0, int c0) {
        int maxDist = max(r0, R - 1 - r0) + max(c0, C - 1 - c0);
        vector<vector<vector<int>>> bucket(maxDist + 1);

        for (int i = 0; i < R; i++) {
            for (int j = 0; j < C; j++) {
                int d = dist(i, j, r0, c0);
                vector<int> tmp = {i, j};
                bucket[d].push_back(move(tmp));
            }
        }
        vector<vector<int>> ret;
        for (int i = 0; i <= maxDist; i++) {
            for (auto &it : bucket[i]) {
                ret.push_back(it);
            }
        }
        return ret;
    }
};

复杂度分析

  • 时间复杂度：$O(RC)$，存储所有点时间复杂度 $O(RC)$，桶排序时间复杂度 $O(RC)$。

  • 空间复杂度：$O(RC)$，需要存储矩阵内所有点。

方法三：几何法

思路及解法

我们也可以直接变换枚举矩阵的顺序，直接按照曼哈顿距离遍历该矩形即可。

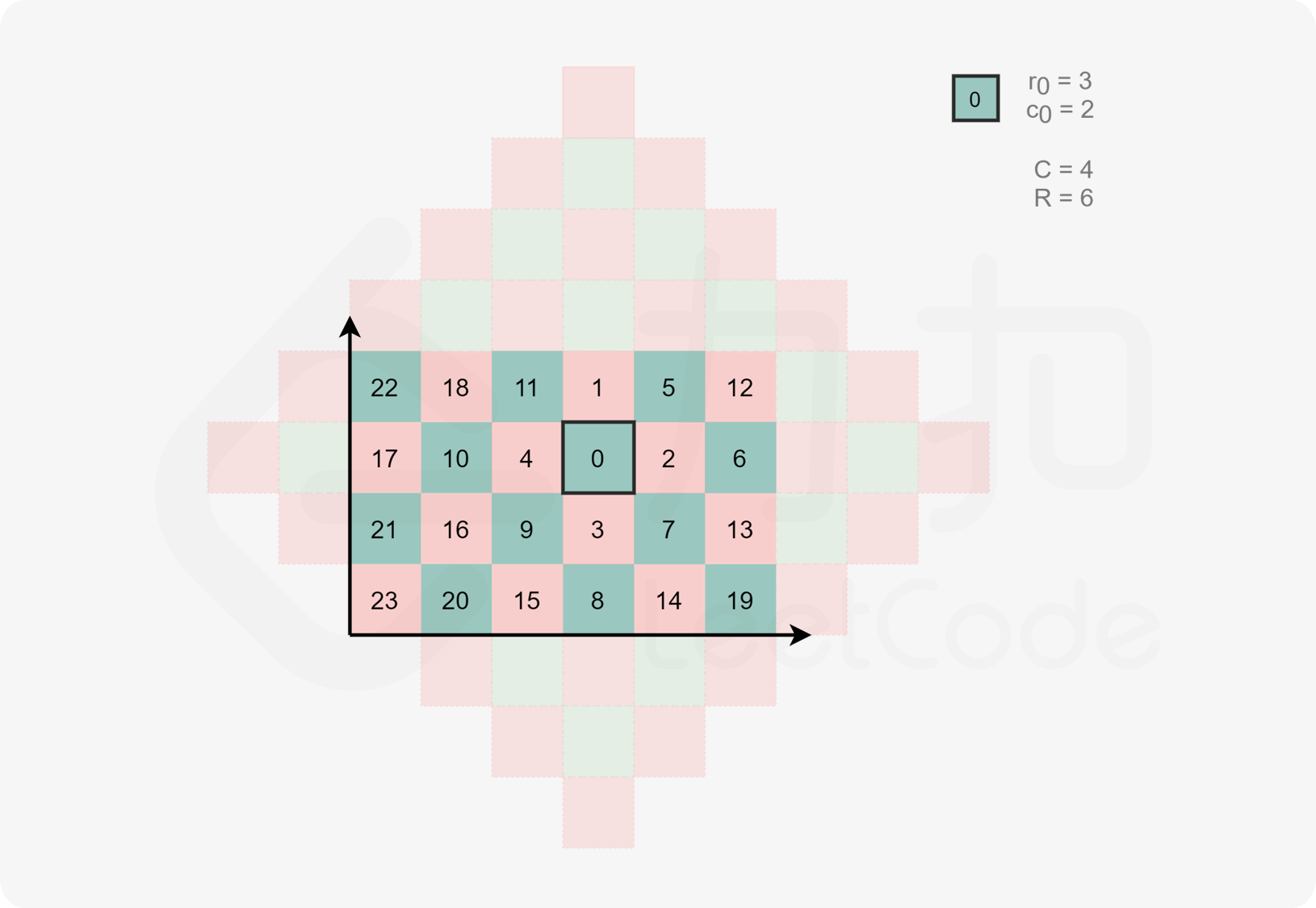
注意到曼哈顿距离相同的位置恰好构成一个斜着的正方形边框，因此我们可以从小到大枚举曼哈顿距离，并使用循环来直接枚举该距离对应的边框。我们每次从该正方形边框的上顶点出发，依次经过右顶点、下顶点和左顶点，最后回到上顶点。这样即可完成当前层的遍历。

fig1

注意正方形边框中的部分点不一定落在矩阵中，所以我们需要做好边界判断。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    const int dr[4] = {1, 1, -1, -1};
    const int dc[4] = {1, -1, -1, 1};

    vector<vector<int>> allCellsDistOrder(int R, int C, int r0, int c0) {
        int maxDist = max(r0, R - 1 - r0) + max(c0, C - 1 - c0);
        vector<vector<int>> ret;
        int row = r0, col = c0;
        ret.push_back({row, col});
        for (int dist = 1; dist <= maxDist; dist++) {
            row--;
            for (int i = 0; i < 4; i++) {
                while ((i % 2 == 0 && row != r0) || (i % 2 != 0 && col != c0)) {
                    if (row >= 0 && row < R && col >= 0 && col < C) {
                        ret.push_back({row, col});
                    }
                    row += dr[i];
                    col += dc[i];
                }
            }
        }
        return ret;
    }
};

复杂度分析

  • 时间复杂度：$O\big((R+C)^2\big)$，我们需要遍历矩阵内所有点，同时也会遍历部分超过矩阵部分的点。在最坏情况下，给定的单元格位于矩阵的一个角，例如 $(0,0)$，此时最大的曼哈顿距离为 $R+C-2$，需要遍历的点数为 $2(R+C-2)(R+C-1)+1$，因此时间复杂度为 $O\big((R+C)^2\big)$。

  • 空间复杂度：$O(1)$，不考虑返回值的空间占用。

⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳总 结⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳
总结：

官方题解直接排序自定义sort排序规则遇到好几次了，自己还是不太会，留作以后补充，桶排序方法也比较常见，至于第三种方法说实话没看懂，作为LeetCode官方题解遗留问题，以后回来做补充。

ps：我要赶紧3道题打完卡去学数学了，啊啊啊😮

------------- THE END! THANKS! -------------