CTF of Z2BNS
0%

位1的个数

发表于 分类于 ，
| 阅读次数： |
Valine：
本文字数： 1.7k 阅读时长 ≈ 2 分钟

题目地址

难度：⭐

题目描述：

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。

提示：

请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的 示例 3 中，输入表示有符号整数 -3。

进阶：

如果多次调用这个函数，你将如何优化你的算法？

示例1：

1
2
3
输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。

示例2：

1
2
3
输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。

示例3：

1
2
3
输入：11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 '1'。

提示：

  • 输入必须是长度为 32 的 二进制串 。
🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️解题过程🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️🙋‍♂️
解题过程：

思路：

这道题和以前做的一道题一样，参考汉明距离，下面给出三种解法，好歹能证明以前那道题咱好好总结了不是😜

①整数转二进制：

题目求二进制表达式中1的个数，我们把整数转二进制，对每位值进行累加。

②与运算按位统计：

每次累加最后一位的值，然后n右移一位。

③与运算1化0：

n&n-1操作可以每次把最后一个1变成0，然后result加1，直到n为0。

方法一：

c++代码：(执行用时0ms，击败100.00%，内存消耗6.1M，击败23.65%）

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int hammingWeight(uint32_t n) {
        int result=0;
        while(n){
            result+=n%2;
            n/=2;
        }
        return result;
    }
};

方法二：

c++代码：(执行用时8ms，击败44.56%，内存消耗6.2M，击败14.35%）

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int hammingWeight(uint32_t n) {
        int result=0;
        while(n){
            result+=n&1;
            n=n>>1;
        }
        return result;
    }
};

方法三：

c++代码：(执行用时4ms，击败44.56%，内存消耗6.3M，击败5.30%）

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int hammingWeight(uint32_t n) {
        int result=0;
        while(n){
            ++result;
            n&=n-1;
        }
        return result;
    }
};
💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎官 方 题 解💎💎💎💎💎💎💎💎💎💎💎💎💎💎💎
官方题解:

方法 1：循环和位移动

算法

这个方法比较直接。我们遍历数字的 32 位。如果某一位是 11 ，将计数器加一。

我们使用 位掩码 来检查数字的第 $i^{th}$位。一开始，掩码 $m=1$因为 $1$的二进制表示是

显然，任何数字跟掩码 $1$ 进行逻辑与运算，都可以让我们获得这个数字的最低位。检查下一位时，我们将掩码左移一位。

并重复此过程

Java代码：

1
2
3
4
5
6
7
8
9
10
11
public int hammingWeight(int n) {
    int bits = 0;
    int mask = 1;
    for (int i = 0; i < 32; i++) {
        if ((n & mask) != 0) {
            bits++;
        }
        mask <<= 1;
    }
    return bits;
}

复杂度分析

  • 时间复杂度：$O(1)$ 。运行时间依赖于数字 $n$ 的位数。由于这题中 $n$ 是一个 32 位数，所以运行时间是 $O(1)$ 的。

  • 空间复杂度：$O(1)$。没有使用额外空间。

方法 2：位操作的小技巧

算法

我们可以把前面的算法进行优化。我们不再检查数字的每一个位，而是不断把数字最后一个 $1$ 反转，并把答案加一。当数字变成 $0$的时候偶，我们就知道它没有 $1$的位了，此时返回答案。

这里关键的想法是对于任意数字 $n$ ，将 $n$ 和 $n - 1$ 做与运算，会把最后一个 $1$ 的位变成 $0$ 。为什么？考虑 $n$ 和 $n - 1$ 的二进制表示。

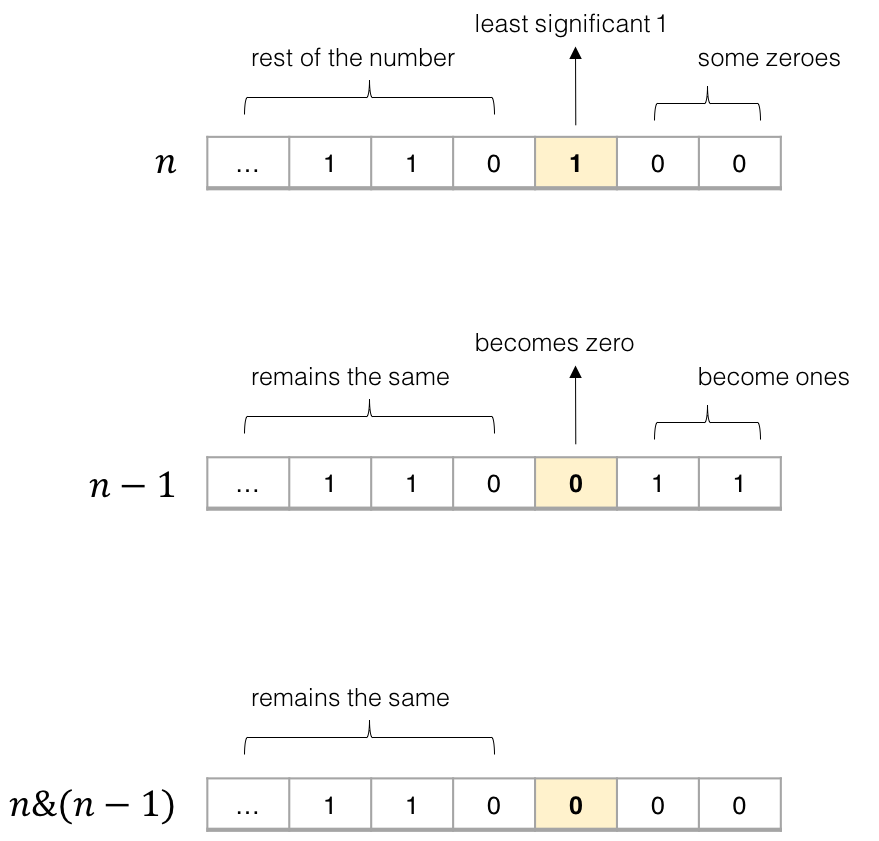
image.png

在二进制表示中，数字 $n$ 中最低位的 $1$ 总是对应 $n - 1$ 中的 $0$ 。因此，将 $n$ 和 $n - 1$与运算总是能把 $n$ 中最低位的 $1$ 变成 $0$ ，并保持其他位不变。

使用这个小技巧，代码变得非常简单。

Java代码：

1
2
3
4
5
6
7
8
public int hammingWeight(int n) {
    int sum = 0;
    while (n != 0) {
        sum++;
        n &= (n - 1);
    }
    return sum;
}

复杂度分析

  • 时间复杂度：$O(1)$。运行时间与 $n$ 中位为 $1$ 的有关。在最坏情况下， $n$ 中所有位都是 $1$ 。对于 32 位整数，运行时间是 $O(1)$ 的。

  • 空间复杂度：$O(1)$。没有使用额外空间。

⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳总 结⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳⏳
总结：

官方题解的两种方法，也就是我的后两种方法，只不过是用Java实现的。其实用不上特别复杂、高大上的东西，用整数转二进制的这么一个直观的方法效率比另两种方法还高，所以不必一味追求高大上，实用型要高🙃。

------------- THE END! THANKS! -------------