CTF of Z2BNS
0%

Logistic映射在图像加密中的应用

发表于 更新于 分类于
| 阅读次数： |
Valine：
本文字数： 1k 阅读时长 ≈ 1 分钟
Logistic映射

Logistic映射是一种可产生的非线性系统，模型表示如下：

式中：$0<\mu\leq4;0<x<1;n∈N;x_n∈[0,1]$；$\mu$是分岔参数，$当3.5699456…<\mu\leq4$时，映射进入混沌(chaos)区域。

Logistic映射分岔图像如下图所示。

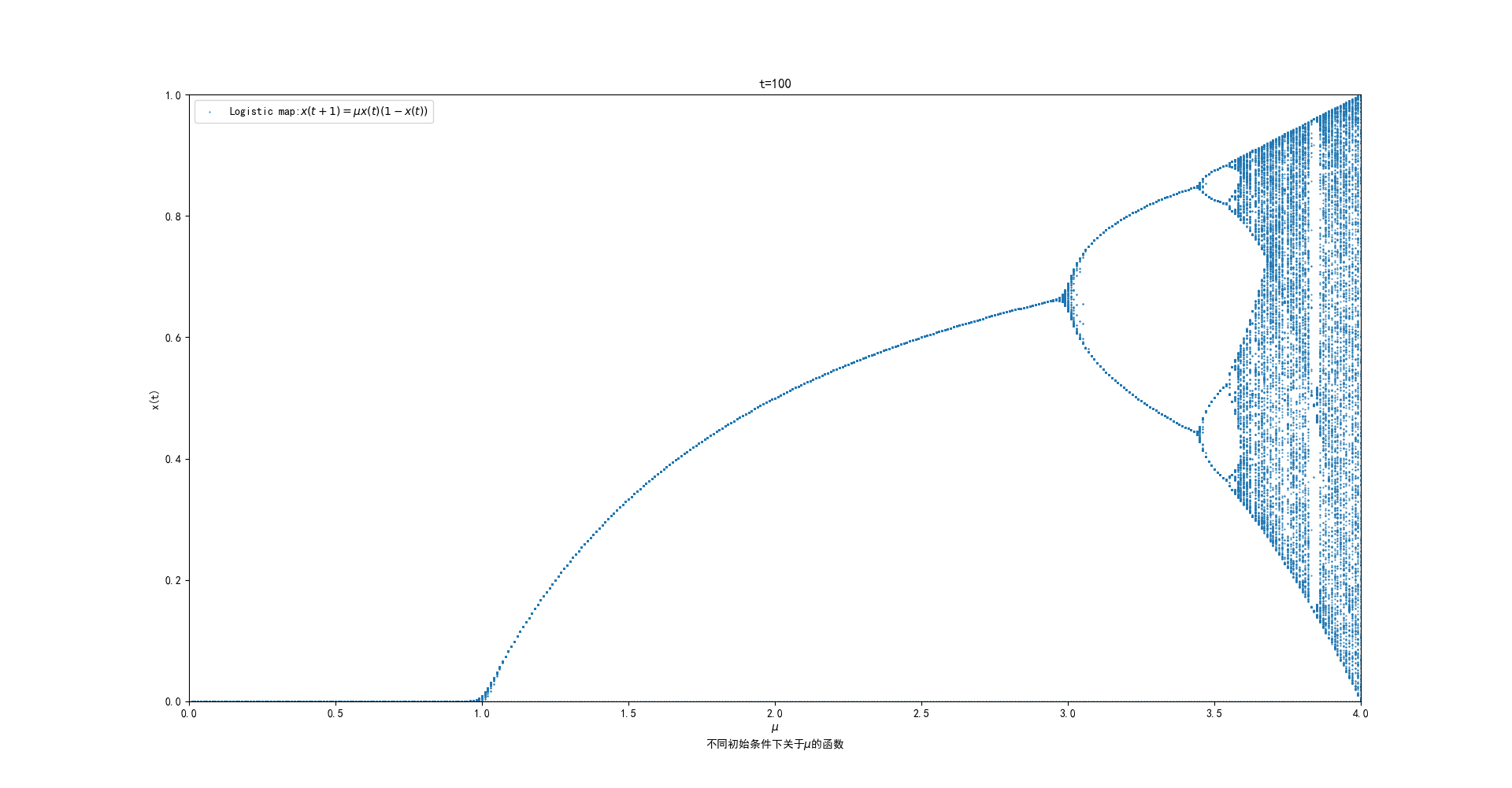
Figure_1

注：

Logistic模型分叉图生成过程及代码见文章尾部参考链接1

混沌方法的数字图像加密实现
摘要

目前混沌系统与加密技术相结合是现如今最热门的一个课题之一，虽然有大量的加密算法面世，但是这些加密算法并不成熟，仍然需要进一步的研究。而混沌系统具有许多重要的性质，如对初始条件和系统参数的敏感依赖性，使得基于混沌系统的图像加密得到了广泛的研究与应用。

虫口模型-Logistic混沌映射

传统的混沌映射加密可分为置换和扩散两个阶段，像素置乱变换与灰度值替换都由混沌系统产生的混沌序列所控制，扩散过程如下：

  • 步骤1:利用混沌序列获取密钥流。
  • 步骤2:加密图像矩阵的像素值。
  • 步骤3:重复步骤2，直到达到密文图像。
算法

设图像(i,j)处的灰度值为I(i,j),满足 $1\leq i \leq M、1\leq j \leq N$, $I’(i,j)$表示替换后 $I(i,j)$在(i,j)出的灰度值。

加密公式：

其中：mod表示求模运算；$\oplus$表示按位异或运算。r1,r2,r3表示的是混沌序列值与255的乘积（采用多混沌序列产生的密钥空间大于单一的混沌序列所产生的密钥空间），替换变换的密钥由r1,r2,r3对应的混沌系统提供，可以进行多次变换寻求更好加密效果。

解密公式：

解密是加密的逆,可以容易得到验证。

实验环境
  • 语言：python3.8
  • 编辑器：Sublime Text 3
  • python库：numpy、matplotlib、cv2
  • 实验图像下载
实验代码（python3.8）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
import cv2
import numpy as np
import matplotlib.pyplot as plt

'''
加密函数
img_encrypt:原始图像(二维ndarray)
key:密钥列表，大小为7(1、2、3为混沌系统初始条件；4、5、6为分岔参数u，7为重复加密次数)
return:返回加密后的图像
'''
def encrypt(img,key):
  #图像的宽高
  [w,h]=img.shape
  #混沌系统初始条件
  x1=key[0]
  x2=key[1]
  x3=key[2]
  #分岔参数u
  u1=key[3]
  u2=key[4]
  u3=key[5]
  #加密次数
  n=key[6]
  #一个临时数组用于返回加密后的图像，可以不影响原始图像
  img_tmp=np.zeros((w,h))
  #对原始图像的每个像素都处理n次
  for k in range(n):
    for i in range(w):
      for j in range(h):
        #计算混沌序列值
        x1=u1*x1*(1-x1)
        x2=u2*x2*(1-x2)
        x3=u3*x3*(1-x3)
        ##混沌值位于[0,1]区间内，所以可以看做是一个系数，乘以最大灰度值并转成整数用于异或运算即可
        r1=int(x1*255)
        r2=int(x2*255)
        r3=int(x3*255)
        img_tmp[i][j]=(((r1+r2)^r3)+img[i][j])%256
    #下一轮加密重新初始化混沌系统
    x1=key[0]
    x2=key[1]
    x3=key[3]
  return img_tmp


'''
解密函数
img:加密后图像(二维ndarray)
key:密钥列表，大小为7(1、2、3为混沌系统初始条件；4、5、6为分岔参数u，7为重复加密次数)
return:返回解密后的图像
'''
def decrypt(img,key):
    #图像的宽高
  [w,h]=img.shape
  #混沌系统初始条件
  x1=key[0]
  x2=key[1]
  x3=key[2]
  #分岔参数u
  u1=key[3]
  u2=key[4]
  u3=key[5]
  #加密次数
  n=key[6]
  #一个临时数组用于返回加密后的图像，可以不影响传入的加密图像
  img_tmp=np.zeros((w,h))
  #对原始图像的每个像素都处理n次
  for k in range(n):
    for i in range(w):
      for j in range(h):
        x1=u1*x1*(1-x1)
        x2=u2*x2*(1-x2)
        x3=u3*x3*(1-x3)
        r1=int(x1*255)
        r2=int(x2*255)
        r3=int(x3*255)
        img_tmp[i][j]=(img[i][j]-((r1+r2)^r3))%256
        # img[i][j]=(img[i][j]-((r1[i*w+j]+r2[i*w+j])^r3[i*w+j]))%256
    #下一轮加密重新初始化混沌系统
    x1=key[0]
    x2=key[1]
    x3=key[3]
  return img_tmp


def main():
  #原始图像路径
  path='./lena.jpg'
  #加密密钥参数列表
  key=[0.343,0.432,0.63,3.769,3.82,3.85,1]
  #读取原始图像
  img=cv2.imread(path)
  #img.shape=>(512,512,3),宽、高、通道数量

  #图像灰度化
  img_gray = cv2.cvtColor(img,cv2.COLOR_RGB2GRAY)
  #混沌加密原始图像
  img_encrypt=encrypt(img_gray,key)
  #错误密钥解密图像
  wrong_key=[0.342,0.432,0.61,3.769,3.82,3.85,1]
  wrong_decrypt=decrypt(img_encrypt,wrong_key)
  #正确密钥解密图像
  img_decrypt=decrypt(img_encrypt,key)

  #结果展示
  plt.rcParams['font.sans-serif'] = ['SimHei']  # 中文乱码
  #子图1，原始图像
  plt.subplot(221)
  #plt默认使用三通道显示图像，所以需要制定cmap参数为gray
  #imshow()对图像进行处理，画出图像，show()进行图像显示
  plt.imshow(img_gray,cmap='gray')
  plt.title('原始图像(灰度化)')
  #不显示坐标轴
  plt.axis('off')

  #子图2，加密后图像
  plt.subplot(222)
  plt.imshow(img_encrypt,cmap='gray')
  plt.title('加密图像(密钥{}'.format(key))
  plt.axis('off')

  #子图3，错误密钥解密结果
  plt.subplot(223)
  plt.imshow(wrong_decrypt,cmap='gray')
  plt.title('解密图像(密钥{})'.format(wrong_key))
  plt.axis('off')

  #子图4，正确密钥解密结果
  plt.subplot(224)
  plt.imshow(img_decrypt,cmap='gray')
  plt.title('解密图像(密钥{})'.format(key))
  plt.axis('off')

  #设置子图默认的间距
  # plt.tight_layout()
  #保存图像
  # cv2.imwrite('./lean_original.jpg',img)
  # cv2.imwrite('./lean_gray.jpg',img_gray)
  # cv2.imwrite('./lean_encrypt.jpg',img_encrypt)
  # cv2.imwrite('./lean_gray.jpg',wrong_decrypt)
  # cv2.imwrite('./lean_decrypt.jpg',img_decrypt)

  #显示图像
  plt.show()


if __name__ == '__main__':
  main()

实验结果

chaos_encrypt

从图中可以看出，哪怕错误密钥与正确密钥只是微小的差别，也难以从解密结果中看出一丝原始图像的信息。采用混沌系统来加密图像取得了较好的效果。

参考：
------------- THE END! THANKS! -------------