Lorenz模型

1963年，Lorenz发现了第一个混沌吸引子——Lorenz系统，从此揭开了混沌研究的序幕。

概念

在数学中，一个动力系统被称为自治的，当且仅当这个系统由一组常微分方程组成，并且这些方程的表达式与动力系统的自变量无关。在有关物理的动力系统中，自变量通常是时间。这时自治系统通常表示其中的物理规律不再随时间变化的系统，也就是说空间中每一点的性质在过去、现在和将来都是一样的。自治系统是动力系统中很重要的一个组成部分。理论上来说，所有的动力系统都可以转化为自治系统。对于自治微分系统来说，要出现混沌现象，其维数必须要大于2.典型的一个例子就是Lorenz模型，它是由美国气象学家Lorenz在研究大气运动的时候，通过对对流模型简化，只保留三个变量提出的一个完全确定性的三阶自治常微分方程组，其方程形式如下：

$\begin{equation} \left\{ \begin{array}{lr} \frac{dx}{dt} =\sigma(y-x) \\ \frac{dy}{dt}=\rho x -y -xz \\ \frac{dz}{dt}=xy-\beta z \end{array} \right . \end{equation}$

其中，三个参数分别为：$\sigma$为普朗特数，$\rho$是瑞利数，$\beta$是方向比。

Lorenz模型已经成为混沌领域的经典模型，系统中三个参数的选择对系统会不会进入混沌状态起着重要的作用。

混沌图像

如图给出了Lorenz模型在 $\sigma=10,\rho=28,\beta=8/3$时系统的三维演化轨迹。

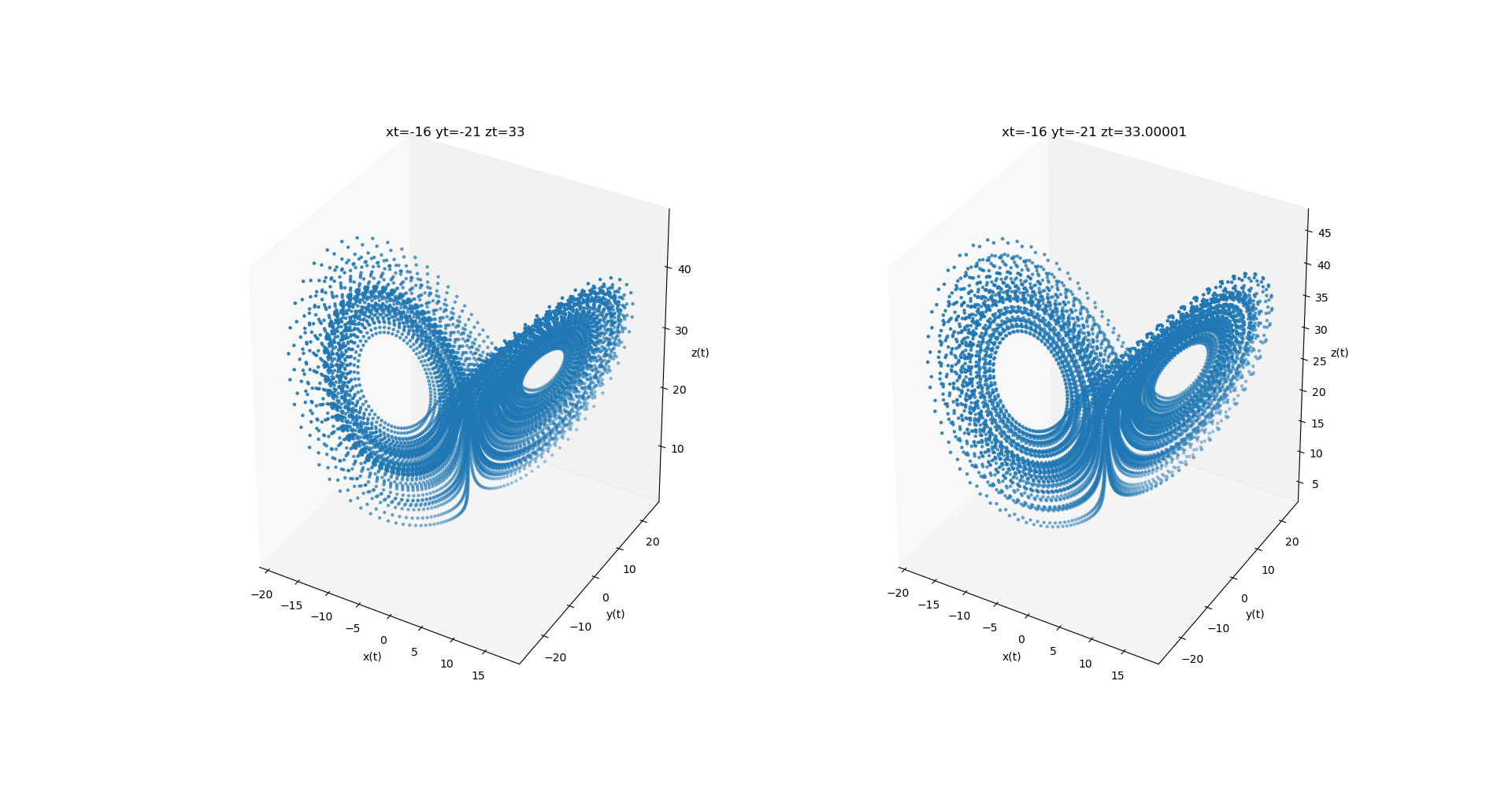
由图可见，经过长时间运行后，系统只在三维空间的一个有限区域内运动，系统在此区域中的运动是混沌状态。我们从两个靠的很近的初值条件出发（zt只相差0.0001）给出了x(t)轨道的演化图如下

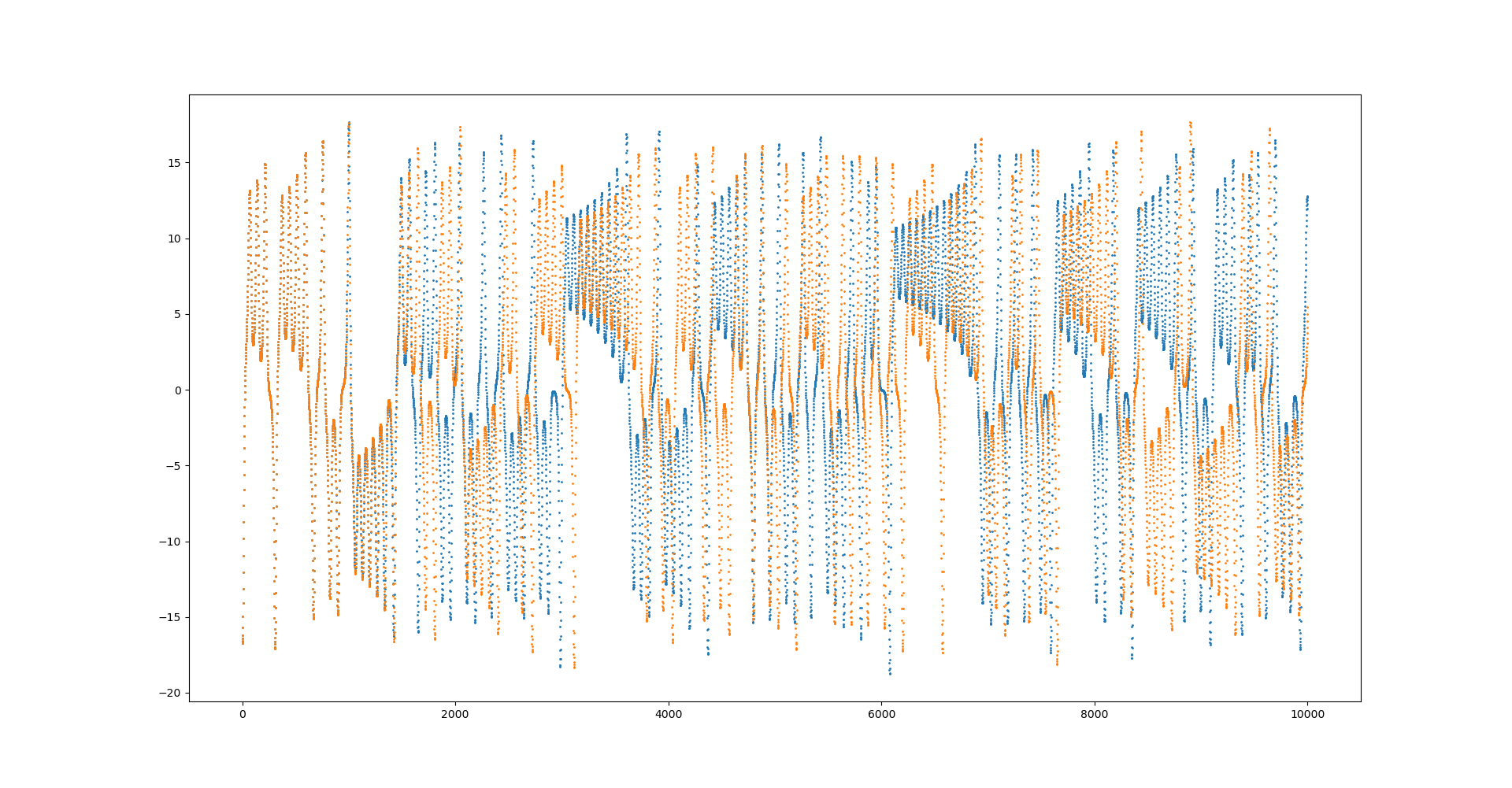
随着时间的演化，可以看到原本靠得很近的轨道迅速地分开，最后两条轨道变得毫无关联，这正是动力学系统对初值敏感性的直观表现，因此我们说此系统的这种状态为混沌态。

实验代码（python）

import matplotlib.pyplot as plt
#绘制三维图像
import mpl_toolkits.mplot3d as p3d

'''
Lorenz吸引子生成函数
参数为三个初始坐标，三个初始参数,迭代次数
返回三个一维list
'''
def Lorenz(x0,y0,z0,p,q,r,T):
  #微分迭代步长
  h=0.01
  x=[]
  y=[]
  z=[]
  for t in range(T):
    xt=x0+h*p*(y0-x0)
    yt=y0+h*(q*x0-y0-x0*z0)
    zt=z0+h*(x0*y0-r*z0)
    #x0、y0、z0统一更新
    x0,y0,z0=xt,yt,zt
    x.append(x0)
    y.append(y0)
    z.append(z0)
  return x,y,z

def main():
  #设定参数
  p=10
  q=28
  r=8/3
  #迭代次数
  T=10000
  #设初值
  x0=-16
  y0=-21
  z0=33
  # fig=plt.figure()
  # ax=p3d.Axes3D(fig)
  x,y,z=Lorenz(x0,y0,z0,p,q,r,T)
  ax=plt.subplot(121,projection="3d")
  ax.scatter(x,y,z,s=5)
  ax.set_xlabel('x(t)')
  ax.set_ylabel('y(t)')
  ax.set_zlabel('z(t)')
  ax.set_title('x0=-16 y0=-21 z0=33')
  # plt.axis('off')
  #消除网格

  ax.grid(False)
  #初值微小的变化
  x0=-16
  y0=-21
  z0=33.00001
  xx,yy,zz=Lorenz(x0,y0,z0,p,q,r,T)
  ax=plt.subplot(122,projection="3d")
  ax.scatter(xx,yy,zz,s=5)
  ax.set_xlabel('x(t)')
  ax.set_ylabel('y(t)')
  ax.set_zlabel('z(t)')
  ax.set_title('x0=-16 y0=-21 z0=33.00001')
  ax.grid(False)
  plt.show()

  t=np.arange(0,T)
  plt.scatter(t,x,s=1)
  plt.scatter(t,xx,s=1)
  plt.show()


if __name__=='__main__':
  main()