CTF of Z2BNS
0%

Rossler模型

发表于 更新于 分类于
| 阅读次数： |
Valine：
本文字数： 744 阅读时长 ≈ 1 分钟

混沌运动是确定性系统中存在随机性，它的运动轨道对初始条件极端敏感。

概念

Rosser给出了一个比Lorenz模型更简单的模型，体现在常微分方程组里只存在一个非线性项，其余都是线性项，它是一个人为构造出来的方程，没有明显的可以对应的物理意义，其具体形式为：

其中，$\omega,\alpha,\beta,\gamma$为系统的参数。我们称 $\omega$为自然频率，是表征系统在没有外界干扰时转动快慢的量。

混沌图像

与Lorenz系统一样，合适的参数才能使系统产生混沌运动。取 $\omega=1.0,\alpha=0.165,\beta=0.2,\gamma=10$，系统混沌吸引子三维形状如图所示

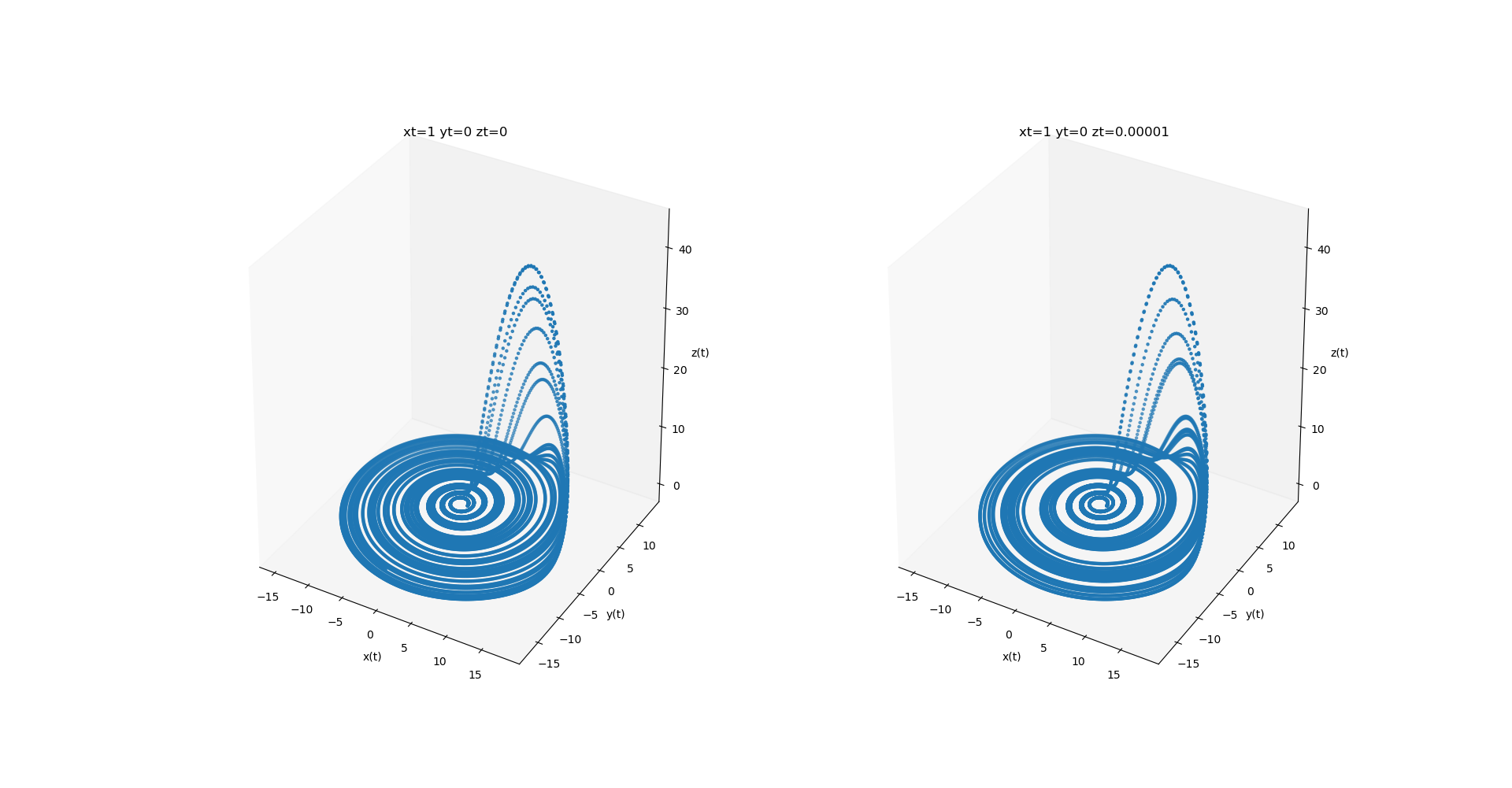
Rossler

从图中可以看出，系统有很好的旋转单心结构并且结构简单，这样简化了混沌系统的同步情况讨论。特别在讨论混沌相同步时，它的单心结构大大简化了关于系统相位的处理，极大地方便了相同步问题的研究，所以Rossler振子在混沌动力学中也是研究比较多的一个模型。

我们从两个靠的很近的初值条件出发（zt只相差0.0001）给出了x(t)轨道的演化图如下

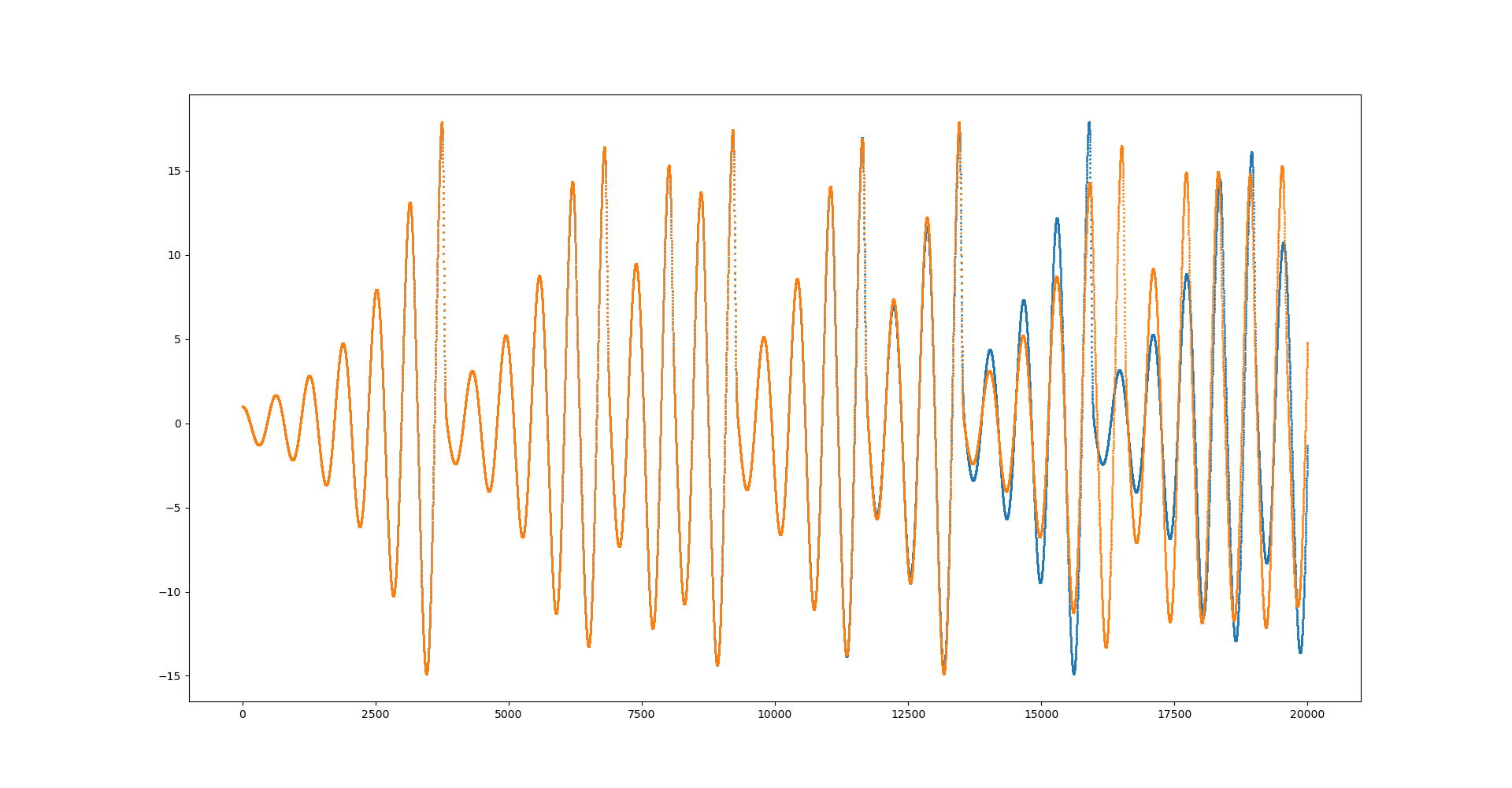
Rossler1

随着时间的演化，可以看到原本靠得很近的轨道迅速地分开，最后两条轨道变得毫无关联，这正是动力学系统对初值敏感性的直观表现，因此我们说此系统的这种状态为混沌态。

实验代码(python)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
import numpy as np
import matplotlib.pyplot as plt
#绘制三维图像
import mpl_toolkits.mplot3d as p3d

'''
Rossler吸引子生成函数
参数为三个初始坐标，四个初始参数,迭代次数
返回三个一维数组(坐标)
'''
def Rossler(x0,y0,z0,w,p,q,r,T):
  h=0.01
  x=[]
  y=[]
  z=[]
  for t in range(T):
    xt=x0+h*(-w*y0-z0)
    yt=y0+h*(w*x0+p*y0)
    zt=z0+h*(q+z0*(x0-r))

    #x0、y0、z0统一更新
    x0,y0,z0=xt,yt,zt
    x.append(x0)
    y.append(y0)
    z.append(z0)
  return x,y,z


def main():
  #设定参数
  w=1
  p=0.165
  q=0.2
  r=10
  #迭代次数
  T=20000
  #设初值
  x0=1
  y0=0
  z0=0
  # fig=plt.figure()
  # ax=p3d.Axes3D(fig)
  x,y,z=Rossler(x0,y0,z0,w,p,q,r,T)
  ax=plt.subplot(121,projection="3d")
  ax.scatter(x,y,z,s=5)
  ax.set_xlabel('x(t)')
  ax.set_ylabel('y(t)')
  ax.set_zlabel('z(t)')
  ax.set_title('x0=1 y0=0 z0=0')
  # plt.axis('off')
  #消除网格
  ax.grid(False)
  #初值微小的变化
  x0=1
  y0=0
  z0=0.00001
  xx,yy,zz=Rossler(x0,y0,z0,w,p,q,r,T)
  ax=plt.subplot(122,projection="3d")
  ax.scatter(xx,yy,zz,s=5)
  ax.set_xlabel('x(t)')
  ax.set_ylabel('y(t)')
  ax.set_zlabel('z(t)')
  ax.set_title('x0=1 y0=0 z0=0.00001')
  ax.grid(False)
  plt.show()
  t=np.arange(0,T)
  plt.scatter(t,x,s=1)
  plt.scatter(t,xx,s=1)
  plt.show()

if __name__=='__main__':
  main()
参考

Lorenz模型

几个混沌系统时间序列数据的Matlab程序

------------- THE END! THANKS! -------------