Chen模型

混沌是非线性动力系统的固有特性，是非线性系统普遍存在的现象。

概念

1999年，美国休斯顿大学陈关荣教授发现了一个新的混沌吸引子——Chen系统，即陈氏混沌系统，它与Lorenz系统类似，但不拓扑等价而且更复杂。Chen系统描述如下：

$$\begin{equation} \left\{ \begin{array}{lr} \frac{dx}{dt} =a(y-x) \\ \frac{dy}{dt}=(c-a) x-xz+cy \\ \frac{dz}{dt}=xy-bz \end{array} \right . \end{equation}$$

陈氏混沌系统(Chen)为典型的混沌系统，当a=35,b=3,c=28时，系统呈现混沌状态。

混沌图像

陈氏混沌吸引子如图所示

由图可见，经过长时间运行后，系统只在三维空间的一个有限区域内运动，系统在此区域中的运动是混沌状态。我们从两个靠的很近的初值条件出发（yt只相差0.001）给出了x(t)轨道的演化图如下

由图可见，随着时间的演化，可以看到原本靠得很近的轨道迅速地分开，最后两条轨道变得毫无关联。

实验代码(python)

import numpy as np
import matplotlib.pyplot as plt
#绘制三维图像
import mpl_toolkits.mplot3d as p3d


'''
Chen吸引子生成函数
参数为三个初始坐标，三个初始参数,迭代次数
返回三个一维数组(坐标)
'''
def Chen(x0,y0,z0,a,b,c,T):
  h=0.001
  x=[]
  y=[]
  z=[]
  for t in range(T):
    xt=x0+h*(a*(y0-x0))
    yt=y0+h*((c-a)*x0-x0*z0+c*y0)
    zt=z0+h*(x0*y0-b*z0)

    #x0、y0、z0统一更新
    x0,y0,z0=xt,yt,zt
    x.append(x0)
    y.append(y0)
    z.append(z0)

  return x,y,z


def main():
  #设定参数
  a=35
  b=3
  c=28
  #迭代次数
  T=10000
  #设初值
  x0=0
  y0=1
  z0=0
  # fig=plt.figure()
  # ax=p3d.Axes3D(fig)
  x,y,z=Chen(x0,y0,z0,a,b,c,T)
  ax=plt.subplot(121,projection="3d")
  ax.scatter(x,y,z,s=5)
  ax.set_xlabel('x(t)')
  ax.set_ylabel('y(t)')
  ax.set_zlabel('z(t)')
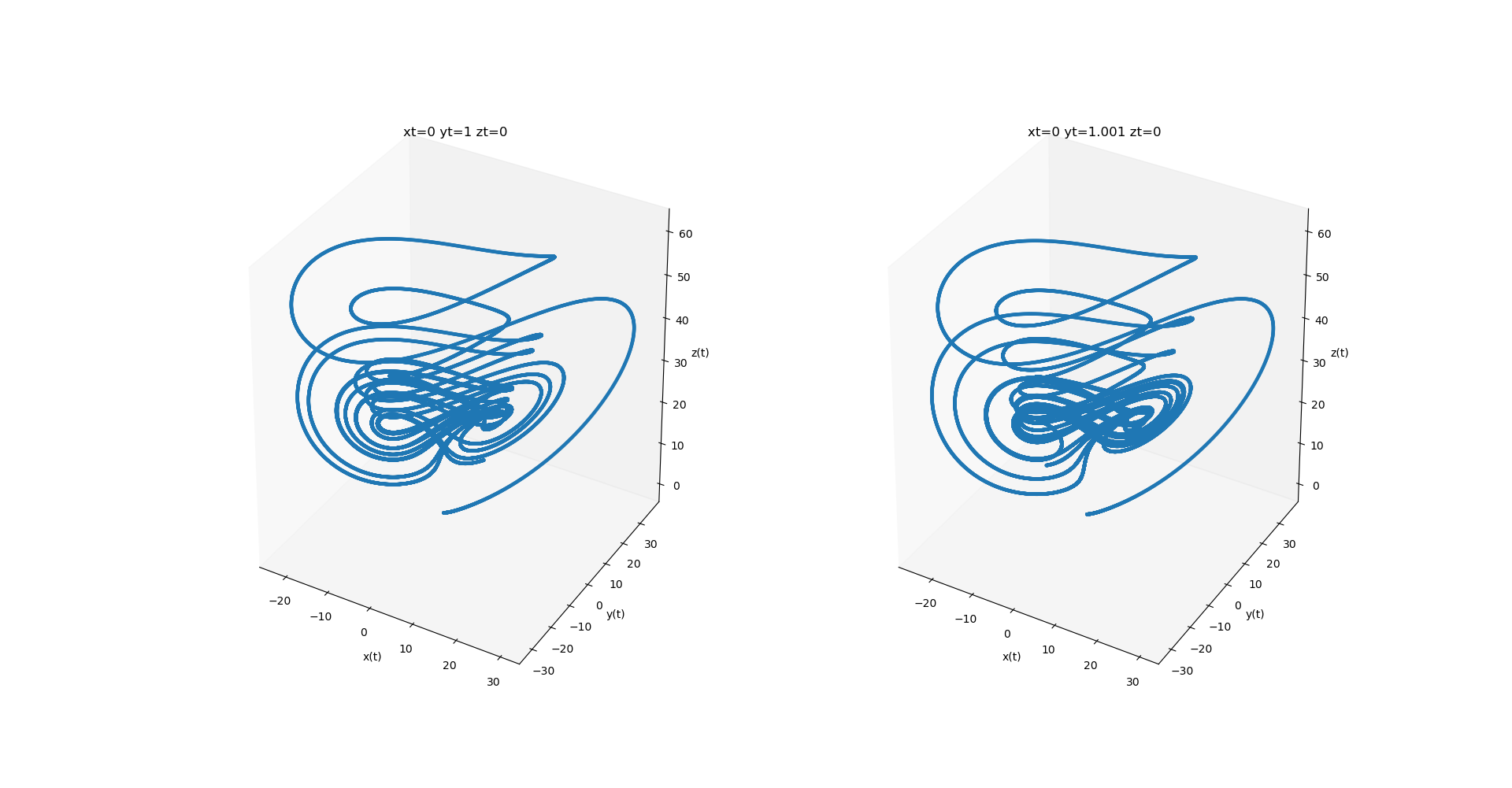
  ax.set_title('x0={0} y0={1} z0={2}'.format(x0,y0,z0))
  # plt.axis('off')
  #消除网格

  ax.grid(False)
  #初值微小的变化
  x0=0
  y0=1.001
  z0=0
  xx,yy,zz=Chen(x0,y0,z0,a,b,c,T)
  ax=plt.subplot(122,projection="3d")
  ax.scatter(xx,yy,zz,s=5)
  ax.set_xlabel('x(t)')
  ax.set_ylabel('y(t)')
  ax.set_zlabel('z(t)')
  ax.set_title('x0={0} y0={1} z0={2}'.format(x0,y0,z0))
  ax.grid(False)
  plt.show()

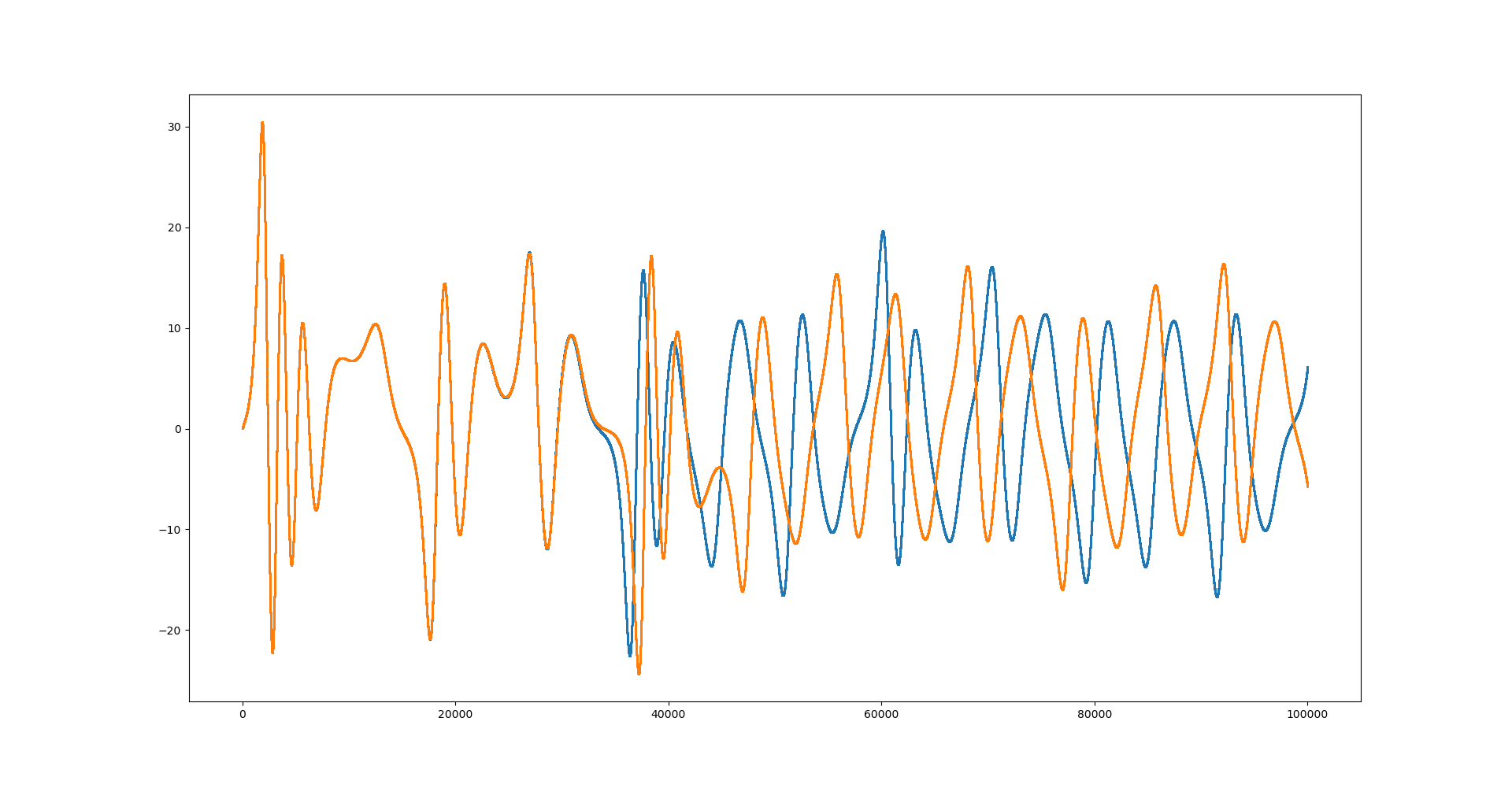
  t=np.arange(0,T)
  plt.scatter(t,x,s=1)
  plt.scatter(t,xx,s=1)
  plt.show()


if __name__=='__main__':
  main()

参考

Lorenz模型

陈氏混沌系统