Color image encryption by using the rotation of color vector in Hartley transform domains

利用hartley变换域旋转彩色向量进行彩色图像加密

摘要

提出了一种基于离散哈特利变换旋转颜色向量加密彩色图像的算法，将彩色图像中的三个分量图像(红、绿、蓝)作为笛卡尔坐标的坐标轴。在图像加密过程中，引入了两种随机角度移位来旋转离散哈特利变换域内由三个颜色分量组成的颜色向量。两个角度对应的旋转位移可以作为方案的密钥。加密后的图像采用实数编码，一些数值模拟已经证明了所提方案的可行性。

引言

自1995年refreger和Javidi提出双随机相位编码技术以来，光学图像加密已成为光学信息安全领域的一个重要课题。一些光学方法被考虑进行加密图像，例如光学转换，干涉术和全息术。

近年来，基于不同随机过程的彩色图像加密方案得到了广泛的研究。为了对彩色图像进行加密，在一些算法中，对红、绿、蓝三种颜色分量分别进行考虑和计算。

本文研究了一种基于离散哈特利变换(DHT)的彩色图像加密算法。将彩色图像的三个颜色分量视为空间坐标的坐标轴。因此，三个元素的颜色向量可以在球坐标下用一个半径和两个角来确定。在DHT的输出平面上，三个颜色分量组成的矢量在原点上通过两次随机独立的角度偏移( $\Delta \theta$ 和 $\Delta \varphi$ )旋转，这两次偏移分别与球坐标下的方位角（$\theta$）和天顶角( $\varphi$ )有关。旋转操作执行两次。最终的加密输出是在DHT域中获得的。加密过程中使用的随机角度偏移是算法的密钥。加密后的图像采用实数编码，便于实际应用中秘密图像的传输和存储。通过数值仿真验证了该加密方法的有效性和有效性。

彩色图像加密算法

随机相位编码技术应用于许多报道的图像加密算法中，是在数学上旋转一个复数。在介绍本文提出的彩色图像加密算法之前，先对彩色图像的三个元素矢量进行旋转运算。

旋转操作

一幅彩色图像可以分解成红、绿、蓝三种颜色的图像。本文将这三种颜色视为空间上的正交坐标轴，如下图所示。

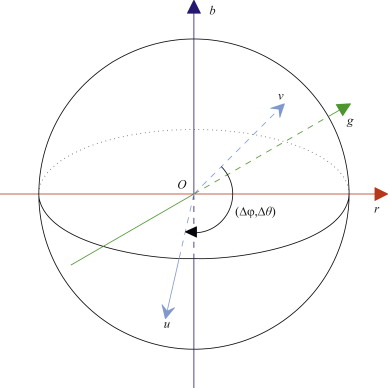
任何颜色都可以表示为用虚线标记的向量v，其等于(r, g, b)。在球坐标系中，$(\rho,\varphi,\theta)$ 等于(r, g, b)，它们的关系可以表示如下：

$\begin{equation} \left\{ \begin{array}{lr} \rho=\sqrt{r^2+g^2+b^2}, \\ \varphi=arccos(b/\rho), \\ \theta=angle(r+ig), \\ \end{array} \ and \ \begin{cases} r=\rho sin\varphi cos\theta, \\ g=\rho sin\varphi sin \theta, \\ b=\rho cos\varphi, \end{cases} \right . \end{equation}$

注：该论文采用的是数学界的球坐标系标记，但 $\theta$为什呢这样表示呢？？

其中，angle符号是用来计算复数的角度的，i是虚数单位。在上图中，根据上式分别用 $\Delta \varphi $和 $\Delta \theta$改变 $\varphi,\theta$使向量v移动到向量u。两个向量(v和u)在旋转操作之前和之后的长度相等。对彩色图像的所有像素进行上述操作完成图像置乱，逆向操作是相同的过程，只是角度变成了 $-\Delta \varphi$和 $-\Delta \theta$。

在旋转操作中存在一种特殊情况，旋转后得到 $\varphi’=\varphi + \Delta \varphi$，该角度大于 $\pi$或者小于0时，就超出了定义范围[0,$\pi$]。为了解决这个问题，定义径向距离 $\widetilde{\rho}$如下：

$\begin{equation} \widetilde{\rho}= \left\{ \begin{array}{lr} \rho·sgn(sin\varphi'), \ if \ sin\varphi'\neq 0, \\ \rho, \ if \ sin\varphi'=0, \\ \end{array} \ \right . \end{equation}$

其中，sgn是符号函数，径向距离 $\widetilde{\rho}$将会应用在图像加密过程中。

旋转操作的计算程序总结如下：

$function \ [I_r’,I_g’,I_b’]=rp_run(I_r,I_g,I_b,\Delta\varphi,\Delta\theta);$

$\rho=\sqrt{I_r.I_r+I_g.I_g+I_b.*I_b};$

$\varphi=arccos(I_b./\rho)+\Delta\varphi;$

$if\ sin\varphi\neq 0$

$\rho=\rho.*sgn(sin\varphi)$

end

$\theta=angle(I_r+i*I_g)+\Delta\theta;$

$I_b’=\rho.*cos(\varphi);$

$I_g’=\rho.sin(\varphi).sin(\theta);$

$I_r’=\rho.sin(\varphi).cos(\theta);$

其中，$(I_r,I_g,I_b)$和 $I_r’,I_g’,I_b’$分别是旋转前后的彩色图像分量。符号‘.*’和’./‘代表两个矩阵相应元素的乘法和除法运算。rp_run函数在图像加密和图像解密过程中都会用到。

加密方案

注：原论文哈特利转换是使用光学系统实现的，鉴于没有光学相关知识和相关条件，就用计算代替（应该可以）。

在该加密方案中引入了哈特利变换，哈特利变换定义如下：

$H_k=\sum_{n=0}^{N-1}{x_n[cos(\frac{2\pi}{N}nk)+sin(\frac{2\pi}{N}nk)]}, \ k=0,...,N-1$

这里变换H将输出一个实输入信号的实结果。哈特利变换的反变换只需将$H_k$视为输入，进行离散哈特利变换，输出再乘上 $\frac{1}{N}$即得。也就是说，离散哈特利反转换除了一个比例因子之外，与离散哈特利转换完全相同。

本文设计的彩色图像加密方案如下图a所示

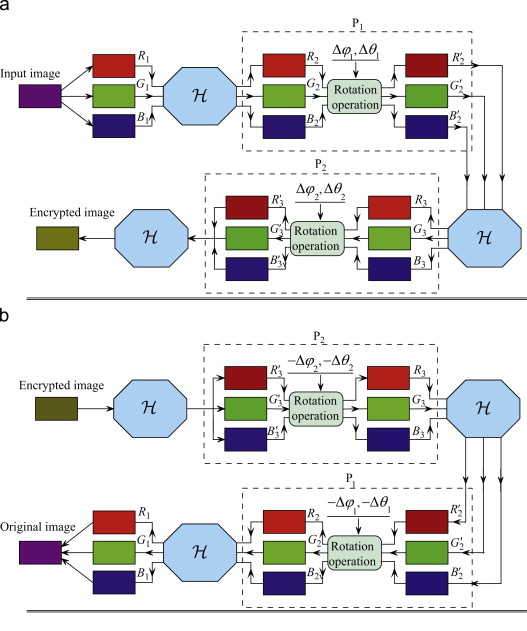
首先，将原始图像分解为3张图像(R1,G1,B1)。在P1块中，使用Hartley变换将这三幅图像转成R2、G2、B2。然后用随机角度 $\Delta\varphi_1$和 $\Delta \theta_1$旋转操作得到图像 $R_2’,G_2’,B_2’$。在P2块中，再次使用DHT变换得到图像 $R_3,G_3,B_3$,使用随机角度 $\Delta\varphi_2$和 $\Delta\theta_2$旋转得到图像 $R_3’,G_3’,B_3’$，最后使用Hartley变换得到加密图像。注意这里的 $\Delta\varphi_1$和 $\Delta\theta_1$各自不等于 $\Delta\varphi_2$和 $\Delta\theta_2$。四个旋转角度 $(\Delta\varphi_1,\Delta\theta_1,\Delta\varphi_2, \Delta\theta_2)$ 是依赖图像像素位置的二维函数。最后合成的图像由实数组成和光学变换领域的一些算法不同。其特点是在实际应用中便于存储和传输加密图像，此外，该算法还可用于三幅相同大小的不同灰度图像的加密。

该加密算法在图像编码中引入了四倍随机角度偏移，提高了秘密信息的安全性。 $(\Delta\varphi_1,\Delta\theta_1,\Delta\varphi_2, \Delta\theta_2)$ 参数可视为提出的加密算法的密钥。