【论文地址 】
一种基于反向二维混沌映射和依赖扩散的图像加密方案 摘要 近年来,人们对各种基于混沌的图像密码系统进行了研究。它们大多采用传统的混淆-扩散体系结构,这种体系结构被认为在应对选择/已知明文攻击是不安全的。本文提出了一种基于依赖扩散和反向猫映射的平面图像非线性遍历方法,以取代传统的在混淆阶段进行线性遍历的方法。设计并实现了两种密码系统。仿真结果和数值分析证明了该方法的有效性和足够的健壮性。
引言 视频、图像、音频等多媒体内容以其通俗易懂、吸引人的表现形式,在日益发展的互联网和移动通信中得到了广泛的传播。某些多媒体文件(如个人视频和图像)通过公共网络传输时,需要保护其隐私。
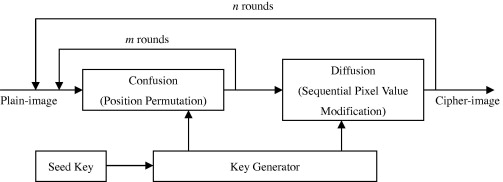
然而,传统的加密系统如DES和AES不适合用于多媒体数据。混沌系统的基本特性,如遍历性,对初始条件和控制参数的敏感性,已经引起了研究人员的注意,因为这些特性可以被认为类似于期望的密码特性。基于混沌的加密算法由于其优越的安全性和复杂性而得到了广泛的研究,1998年,Fridrich首先提出了一种基于混沌的由置换和扩散组成的图像密码系统。在这种结构下,明文图像像素的排列由二维混沌映射控制,如standard映射、baker映射和cat映射。在扩散阶段,通常采用一维混沌映射,其图像加密结构如下图所示。
friedrich结构已经成为许多后来提出的基于混沌的图像加密算法中最流行的结构。
混淆和扩散有多种方法,Wang等人指出,在固定参数的confusion-diffusion架构下,如果是同一像素的均匀图像,这两个过程就会变得独立,在这种情况下,混淆效应被消除,整个密码系统的安全性只依赖于扩散。因此,可以得出结论,可以通过以下步骤来攻击Fridrich混淆-扩散结构:(1)选择具有相同像素的均匀图像来消除混淆的影响(2)扩散阶段的密钥流通过已知明文攻击或选择明文攻击获得(3)剩余的密码图像可以看作是一种纯置换密码的输出,这种密码已经被证明是不安全的,并且可以很容易地通过已知明文或选择明文攻击进行密码分析。
本文设计了两种密码系统来避免Fridrich体系结构的缺陷。第一个使用了依赖扩散和反向cat映射。由于混淆阶段和扩散阶段之间没有明确的划分,它可以被认为是Fridrich框架的一个改进版本。因此,克服了传统架构的缺点。在Fridrich架构中,在像素值扩散之前,所有像素都被排列。这意味着混淆和扩散操作的基本单位是整个图像。然而,在我们的方案中,基本单位是像素,一旦一个像素的新位置被计算出来,我们立即扩散像素,而不是计算下一个像素的位置。加密后像素的值影响下一个像素的混淆和扩散操作,混淆效应支配着像素级的扩散过程。因此,我们只需要对所有像素进行一次遍历,而不是像传统结构中那样由一个混乱和一个扩散组成的两次遍历。因此,该方案具有更高的效率。
在第二种提出的密码系统中,在混沌阶段采用基于二维混沌映射的改进映射,在同一阶段进行简单扩散。在传统的混淆过程中,定义了一个从普通位置到伪随机位置的映射。以cat map为例,该map的输入序列为常规像素位置(通常从左上角到右下角),而输出序列为伪随机序列。本文提出了一种新的映射方法,将明文图像中的一个伪随机位置映射到密文图像中的另一个伪随机位置。在新的映射操作和混淆阶段的简单扩散的帮助下,混淆和扩散效果不能使用相同像素的明文图像分离。因此,对纯排列密码的密码分析变得无效。
依赖扩散 在传统的置乱—扩散型图像密码系统中,这两个过程是独立进行的。首先,计算每个像素点的新位置,然后在扩散阶段对像素值进行更改,在这种结构下,需要对所有像素进行两轮遍历。为了减少执行时间,我们研究了混淆和扩散是否可以只通过遍历一次像素来执行。在提出的方案中,使用反向cat映射进行依赖扩散和像素重定位,当计算一个像素的位置时,它的值也是通过依赖扩散得到的。采用了cat映射和Logistic映射,并且只需要一轮遍历所有像素。对每一个像素,采用下式1计算它的新位置,然后使用下式2扩散像素。然而,在Fridrich体系结构中,所有像素的位置在扩散操作开始之前计算。依赖扩散的公式如下:
在式1中,(x,y)是明文图像像素的原始位置,(x’,y’)是cat映射产生的伪随机位置,p、q是cat映射的两个参数,N是方形图像的高或宽。在式2中,arr(x,y)和ciphered(x’,y’)分别是明文图像和密文图像的像素值。此外,t是前一个处理的像素值,$\alpha$是Logistic映射参数。
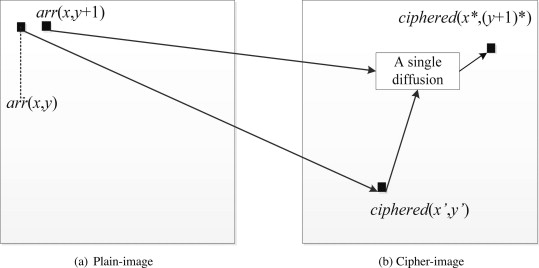
如果扩散过程是按顺序进行的,或者正在处理的像素的值不受前一个像素的影响,密码系统对普通图像的轻微修改将变得不敏感。在使用普通cat映射的依赖扩散中,被处理的像素与加密图像中之前处理的像素不相邻,如下图所示,变量t用来存储之前处理过的像素值。
为了清楚地说明使用普通cat映射依赖扩散的概念,首先选择两个像素,如arr(x,y)和arr(x,y+1)是两个明文图像中的相邻像素,ciphered(x’,y’),ciphered(x*,(y+1)*)是加密图像中两个相应的不相邻的加密像素。首先,计算arr(x,y)的新位置(x’,y’)。然后执行这个像素的扩散过程,得到新的像素值ciphered(x’,y’)。临时变量t设置为ciphered(x’,y’)。第二步,计算arr(x,y+1)的新位置(x*,(y+1)*),然后进行扩散过程,该过程受之前处理的像素t的影响。
在依赖扩散体系结构中,混淆的参数和初始值(或混淆的影响)决定了像素之间的扩散顺序,密码图像的像素值既受扩散阶段密钥的影响,又受之前处理过的像素值的影响。当前的像素和之前处理的像素之间的关系由临时变量t控制,以增加对普通图像中任何修改的敏感性。
反向使用2维混沌映射 在大多数经典的图像密码系统中,混沌阶段通常采用二维混沌映射,以cat映射为例,在混乱阶段,几乎所有的像素都被映射重新定位,它定义了从原始位置(通常是左上角到右下角)到伪随机位置的映射。当混淆阶段开始时,明文图像不同位置的像素有不同的处理顺序。例如左上角像素arr(0,0)总是第一个被处理的,右下角位置arr(511,511)是最后一个被处理的。
明文图像中一个像素的处理顺序是重要的,假设cat映射的输出序列是伪随机的,我们可以研究是否有可能反向使用映射以非线性的方式而不是常规的方式来访问明文图像像素。如果cat映射定义了从原始位置到伪随机位置的映射,那么反向cat映射应该给出从伪随机位置到常规位置的映射。几乎所有的像素都有相同的概率被重新定位到处理序列中的任何位置,这意味着最后一个像素arr(511,511)将不总是处理序列中的最后一个。依赖扩散反向cat映射公式定义如下
反向和普通cat映射的区别是像素位置,一个是ciphered(x’,y’)和arr(x,y),另一个是ciphered(x,y)和arr(x’,y’)。例如,arr(511,511)轻微改变,像素将会在更早的阶段处理不是最后一个。像素序列将会被早期阶段极小的改变影响。
如图描述了普通二维混沌映射和反向使用混沌映射在混淆效应上的区别。
图中,像素1,2,3,4是明文图像像素,像素1’,2’,3’,4’是密码图像中的排列后的像素,图1使用了普通的二维混沌映射,相邻像素按顺序访问然后被映射到伪随机位置。然而,反向使用2维混沌映射时明文图像中的像素由参数和初始值决定的映射的输出伪随机序列来控制,然后映射到密文图像中的普通位置。除了cat映射之外,standard映射、henon映射、baker映射也可以用在依赖扩散阶段。基于以上分析,我们可以研究一种新的映射,即从普通图像中的一个伪随机位置到密码图中的另一个伪随机位置,可以结合普通映射和反向使用二维混沌映射来定义。
相同像素值明文图像的混淆效果 ???没看懂
提出方案 算法1 在算法1中,应用了反向cat映射和依赖扩散,算法结构如下图所示:
依赖扩散由反向cat映射和Logistic映射控制。普通cat映射公式见上文,Logistic定义如下:
其中,$\alpha$是逻辑映射系数。当 $\alpha\in [3.57,4]$时,输出序列是混沌的。两个序列SQ1和SQ2由Logistic系统产生,初始值为conf_key1=0.12345678912345和conf_key2=0.67856746347633, $\alpha$被设置为3.99999。
pi和qi为第i轮依赖扩散的反向cat映射的系数,$r_x^j,r_y^j$是在第j轮加密中随机选择的像素位置。这四个参数计算如下:
依赖扩散过程由下面这组式子控制
其中,t是一个临时变量用来存储前一个加密像素值。它的初始值定义为:$t=[4key_d (1-key_d)*1000]mod 256$,N是测试图像的宽或高,$x\in[0,N-1],y\in[0,N-1]$,key_d被设置为0.33456434300001。arr(x’,y’)表示明文图像在随机位置(x’,y’)处的像素。ciph(x,y)代表密文图像(x,y)位置处的像素。(pi,qi)是第i轮依赖扩散中反向cat映射的系数对,i=1,2,…,m。本文使用依赖扩散轮数为2。
提出方案的操作流程描述如下:
步骤1:生成随机对 $(r_x^j,r_y^j)$
步骤2:交换像素arr(0,0)和 $(r_x^j,r_y^j)$来解决cat映射中的不动点问题
步骤3:进行m轮依赖扩散
第i轮(i=1,2,…,m)过程如下
(1)计算出(pi,qi)
(2)根据反向cat映射(参数为(pi,qi))生成随机位置(x’,y’),在扩散操作中修改明文图像arr(x’,y’)的值。每一个加密像素的值都被两个因素影响:arr(x’,y’)和前一个加密像素的值
(3)加密像素被密文图像常规位置(x,y)的值替换
步骤4:回到第二步继续执行知道明文图像的所有像素都被加密
在该方案中,两轮不同系数和初始值的相关扩散形成一轮加密。仿真结果表明,仅在两轮加密中,NPCR和UACI值即可分别达到99.6%和33.4%。
算法2 普通的cat映射定义了一个从普通位置到伪随机位置的映射,而反向的cat映射给出了一个从伪随机位置到常规位置的映射。将普通cat映射和反向cat映射相结合,能否得到一种新的伪随机位置到另一伪随机位置的映射,是值得研究的问题。
在使用普通cat映射的扩散阶段,输入对(xi,yi)通常表示明文图像中的像素位置,处理顺序通常是从左上角到右下角。同时,cat映射的输出位置 $(r_{xi},r_{yi})$被认为是伪随机的。cat映射的混淆效果实现是通过映射明文图像中的每一个像素从(xi,yi)到相应的密文图像中的伪随机位置 $(r_{xi},r_{yi})$。
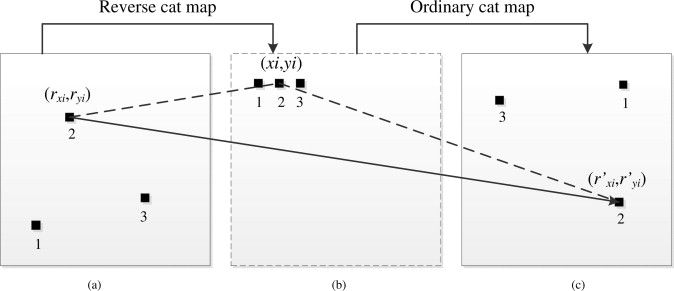
反向cat映射的情况恰好相反,混淆效果实现是通过映射明文图像中 $(r_{xi},r_{yi})$处的像素到密文图像中 $(x_i,y_i)$处的像素。由于两种映射操作的不同特点,将普通cat映射和反向cat映射相结合,可以得到一种新的伪随机位置到另一伪随机位置的混淆映射,如下图所示
其中,a是明文图像,c是扩散之后的密文图像,b是排列阶段的转换中间图像。(p1,q1)是在第一次扩散步骤中(从a到b)反向cat映射的参数对,(p2,q2)表示第二次扩散步骤中(从b到c)普通cat映射的参数。在新扩散过程中有四个参数而不是两个控制着从伪随机位置到另一个伪随机位置的映射。
首先,使用反向cat映射生成一个随机位置 $(r_{xi},r_{yi})$,明文图像中这个位置的像素指向临时位置(xi,yi)的像素。第二,使用cat映射去映射(xi,yi)位置的像素到另一个随机位置 $(r_{xi}’,r’_{yi})$。以像素2为例,开始位置和最终位置被(p1,q1)和(p2,q2)控制。注意图中b在扩散阶段不是真的存在,只是一个转换过渡状态。
同样的混淆效果也可以通过组合两个不同的二维混沌映射实现,例如反向standard映射和普通cat映射结合或者反向cat映射和普通baker映射结合。
在算法2中,采用了friedrich结构,并进行了以下修改,以避免上述缺陷:(1)混淆阶段由反向和普通cat映射组成;(2)在两个混淆步骤之间进行像素值修改,混淆阶段由下式控制,其中rand1是一个由Logistic生成的有256个元素的随机数序列,初始值和控制参数分别为0.72345678912345和3.99999。如果在计算rand1时,输出数与前面的任何一个相同,就拒绝该数字,继续进行下一轮计算以确保rand1中没有相同的数字。舍弃Logistic映射生成的前2000个数字,temp1是一个临时变量,存储处理后的像素值。
其中,temp1的初始值被设置为$temp1={[3.99999(conf_key5) (1-conf_key5)]*10^3}mod 256$。SQ3和SQ4由Logistic映射生成,初始值分别为conf_key3和conf_key4。pi和qi根据下式进行计算。
conf_key3,conf_key4和conf_key5分别被设置为0.12345678912340,0.88795676859468和0.12345432167893。arr(x’,y’)是用反向cat映射在明文图像中随机选择的在(x’,y’)处的像素值。mid(x,y)代表临时位置,ciph(x’’,y’’)是在扩散操作后(x’’,y’’)位置处的加密像素的值。
在算法2的扩散操作中应用下面式子去扩散中间图像。在式子中,rand2是和rand1同样的计算方式得到的。Logistic映射初始值和系数分别设置为 0.33798657654353和3.99999。
在上式中,temp2的初始值被设置为 $temp2={[3.99999(key_d1) (1-key_d1)]*10^3}mod\ 256$,key_d1被选择为0.54567894324298,ac(i)代表在扩散阶段获得的一维序列中第i个像素值,ciph_d(i)是扩散之后第i个像素值,temp2是临时变量存储处理后的像素值。
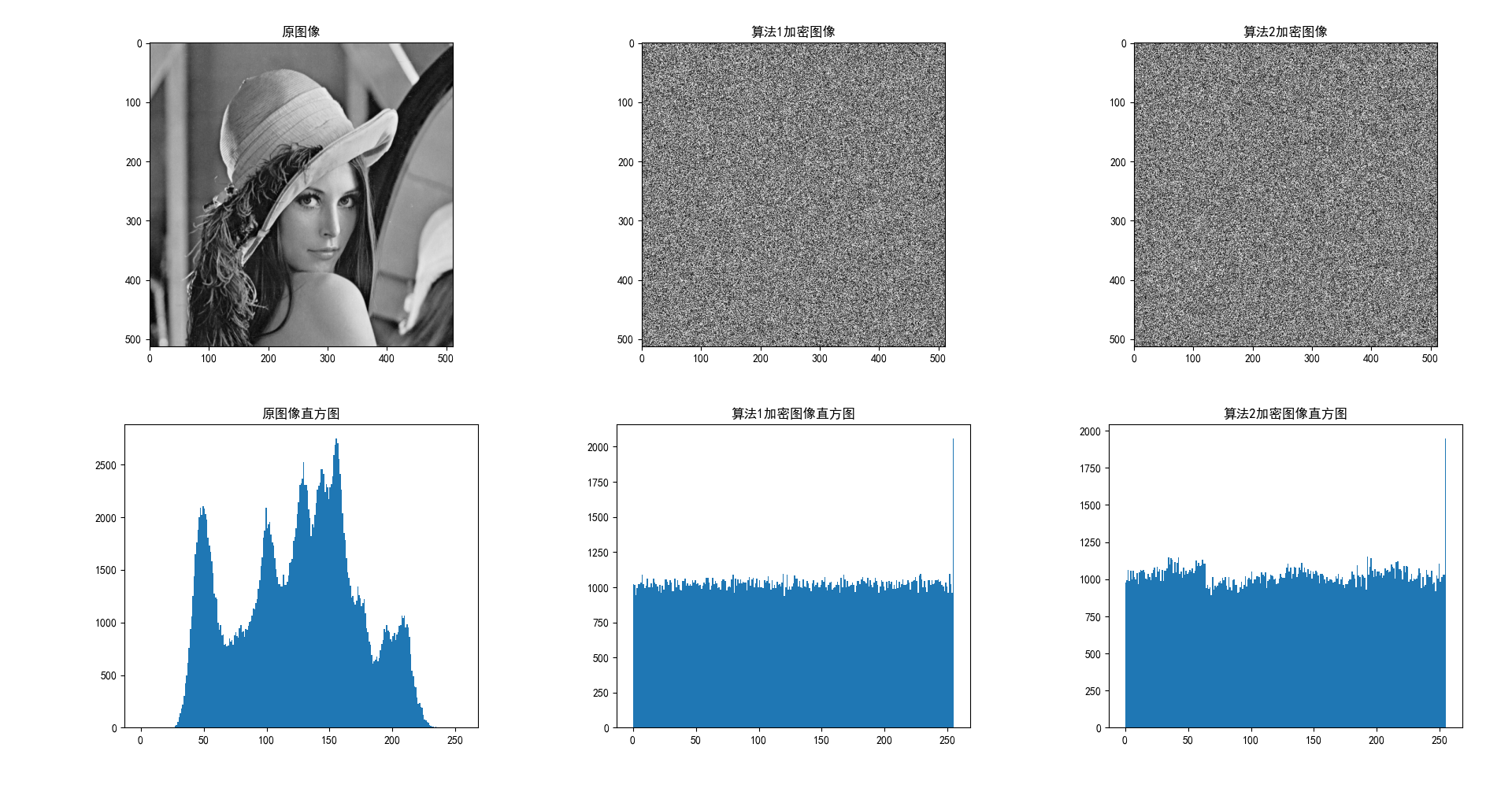
实验结果 实验采用512*512的灰度Lena图像进行测试,加解密结果如下。
算法1(反向cat 映射和依赖扩散)加解密结果:
算法2(反向cat map和普通cat map以及依赖扩散)
实验代码 算法1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 import cv2import hashlibimport numpy as npimport matplotlib.pyplot as pltdef Logistic (x0,T,u=3.99999 ): seq=np.zeros(T) for i in range(T): x0=u*x0*(1 -x0) seq[i]=x0 return seq ''' 算法1加密函数 img:加密图像路径 key:密钥列表,大小为6(1、2、3为Logistic初始条件和参数;4、5为加密轮数和扩散轮数,6为异或扩散时的参数) return:返回加密后的图像 ''' def encrypt (img,key ): im=cv2.imread(img,-1 ) h,w=im.shape n=key[3 ] m=key[4 ] conf_key1=key[0 ] conf_key2=key[1 ] a=key[2 ] key_d=key[5 ] T=2000 +100 +m+n seq1=Logistic(conf_key1,T,a) seq2=Logistic(conf_key2,T,a) for j in range(n): rx=int(seq1[2000 +100 +j]*(10 **9 ))%h ry=int(seq2[2000 +100 +j]*(10 **9 ))%w tmp=im[rx][ry] im[rx][ry]=im[0 ][0 ] im[0 ][0 ]=tmp ciph=np.zeros((h,w),dtype=np.uint8) for i in range(m): pi=int(seq1[2000 +i]*(10 **9 ))%h qi=int(seq2[2000 +i]*(10 **9 ))%w t=int(4 *key_d*(1 -key_d)*1000 )%256 for x in range(h): for y in range(w): x1=int(x+pi*y)%h y1=int(qi*x+(pi*qi+1 )*y)%w ciph[x][y]=np.bitwise_xor(im[x1][y1],int(a*(t/1000 )*(1 -(t/1000 ))*1000 )%256 ) t=ciph[x][y] im=np.array(ciph) return ciph ''' 算法1解密函数 img:加密图像路径 key:密钥列表,大小为6(1、2、3为Logistic初始条件和参数;4、5为加密轮数和扩散轮数,6为异或扩散时的参数) return:返回解密后的图像 ''' def decrypt (img,key ): ciph=cv2.imread(img,-1 ) h,w=ciph.shape n=key[3 ] m=key[4 ] conf_key1=key[0 ] conf_key2=key[1 ] a=key[2 ] key_d=key[5 ] T=2000 +100 +m+n seq1=Logistic(conf_key1,T,a) seq2=Logistic(conf_key2,T,a) for j in range(n-1 ,-1 ,-1 ): rx=int(seq1[2000 +100 +j]*(10 **9 ))%h ry=int(seq2[2000 +100 +j]*(10 **9 ))%w plain=np.zeros((h,w),dtype=np.uint8) for i in range(m-1 ,-1 ,-1 ): pi=int(seq1[2000 +i]*(10 **9 ))%h qi=int(seq2[2000 +i]*(10 **9 ))%w t=int(4 *key_d*(1 -key_d)*1000 )%256 for x in range(h): for y in range(w): x1=int(x+pi*y)%h y1=int(qi*x+(pi*qi+1 )*y)%w plain[x1][y1]=np.bitwise_xor(ciph[x][y],int(a*(t/1000 )*(1 -(t/1000 ))*1000 )%256 ) t=ciph[x][y] ciph=np.array(plain) tmp=plain[rx][ry] plain[rx][ry]=plain[0 ][0 ] plain[0 ][0 ]=tmp return plain def main (): img_path='./Lena.jpg' img=cv2.imread(img_path,-1 ) key=[] conf_key1=0.12345678912345 conf_key2=0.67856746347633 a=3.99999 n=1 m=2 key_d=0.33456434300001 key.append(conf_key1) key.append(conf_key2) key.append(a) key.append(n) key.append(m) key.append(key_d) img=cv2.imread(img_path,-1 ) img_encrypt=encrypt(img_path,key) cv2.imwrite('./Lena_encrypt.png' ,img_encrypt) encrypt_path='./Lena_encrypt.png' img_decrypt=decrypt(encrypt_path,key) decrypt_path='./Lena_decrypt.png' cv2.imwrite(decrypt_path,img_decrypt) wrong_key=list(key) wrong_key[0 ]+=pow(10 ,-10 ) wrong_decrypt=decrypt(encrypt_path,wrong_key) cv2.imwrite('./wrong_decrypt.png' ,wrong_decrypt) plt.rcParams['font.sans-serif' ] = ['SimHei' ] plt.subplot(221 ) plt.imshow(img,cmap='gray' ) plt.title('原始图像' ) plt.axis('off' ) plt.subplot(222 ) plt.imshow(img_encrypt,cmap='gray' ) plt.title('加密图像\nconf_key1={}' .format(key[0 ])) plt.axis('off' ) plt.subplot(223 ) plt.imshow(wrong_decrypt,cmap='gray' ) plt.title('解密图像\nconf_key1={}' .format(wrong_key[0 ])) plt.axis('off' ) plt.subplot(224 ) plt.imshow(img_decrypt,cmap='gray' ) plt.title('解密图像\nconf_key1={}' .format(key[0 ])) plt.axis('off' ) plt.tight_layout() plt.show() if __name__ == '__main__' : main()
算法2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 import cv2import hashlibimport numpy as npimport matplotlib.pyplot as pltdef Logistic (x0,T,u=3.99999 ): seq=np.zeros(T) for i in range(T): x0=u*x0*(1 -x0) seq[i]=x0 return seq ''' 算法2加密函数 img:加密图像路径 key:密钥列表,大小为6(1、2、3为Logistic初始条件和参数;4、5为加密轮数和扩散轮数,6为异或扩散时的参数) return:返回加密后的图像 ''' def encrypt (img,key ): im=cv2.imread(img,-1 ) h,w=im.shape conf_key3=key[0 ] conf_key4=key[1 ] rand1_key=key[2 ] rand2_key=key[3 ] a=key[4 ] conf_key5=key[5 ] key_d1=key[6 ] T=2000 +3 seq3=Logistic(conf_key3,T,a) seq4=Logistic(conf_key4,T,a) p1=int(seq3[2001 ]*(10 **9 ))%h q1=int(seq4[2001 ]*(10 **9 ))%w p2=int(seq3[2002 ]*(10 **9 ))%h q2=int(seq4[2002 ]*(10 **9 ))%w rand1={} rand2={} i=0 while len(rand1)<256 : rand1_key=a*rand1_key*(1 -rand1_key) rand1[int(rand1_key*1000 )%256 ]=1 rand1=list(rand1.keys()) while len(rand2)<256 : rand2_key=a*rand2_key*(1 -rand2_key) rand2[int(rand2_key*1000 )%256 ]=1 rand2=list(rand2.keys()) mid=np.zeros((h,w),dtype=np.uint8) ciph=np.zeros((h,w),dtype=np.uint8) temp1=int(3.99999 *conf_key5*(1 -conf_key5)*1000 )%256 temp2=int(3.99999 *key_d1*(1 -key_d1)*1000 )%256 for x in range(h): for y in range(w): x1=int(x+p1*y)%h y1=int(q1*x+(p1*q1+1 )*y)%w mid[x][y]=im[x1][y1]^rand1[temp1] mid[x][y]=mid[x][y]^rand2[temp2] temp2=mid[x][y] x2=int(x+p2*y)%h y2=int(q2*x+(p2*q2+1 )*y)%w ciph[x2][y2]=mid[x][y] temp1=ciph[x2][y2] return ciph ''' 算法2加密函数 img:加密图像路径 key:密钥列表,大小为6(1、2、3为Logistic初始条件和参数;4、5为加密轮数和扩散轮数,6为异或扩散时的参数) return:返回加密后的图像 ''' def decrypt (img,key ): ciph=cv2.imread(img,-1 ) h,w=ciph.shape conf_key3=key[0 ] conf_key4=key[1 ] rand1_key=key[2 ] rand2_key=key[3 ] a=key[4 ] conf_key5=key[5 ] key_d1=key[6 ] T=2000 +3 seq3=Logistic(conf_key3,T,a) seq4=Logistic(conf_key4,T,a) p1=int(seq3[2001 ]*(10 **9 ))%h q1=int(seq4[2001 ]*(10 **9 ))%w p2=int(seq3[2002 ]*(10 **9 ))%h q2=int(seq4[2002 ]*(10 **9 ))%w rand1={} rand2={} i=0 while len(rand1)<256 : rand1_key=a*rand1_key*(1 -rand1_key) rand1[int(rand1_key*1000 )%256 ]=1 rand1=list(rand1.keys()) while len(rand2)<256 : rand2_key=a*rand2_key*(1 -rand2_key) rand2[int(rand2_key*1000 )%256 ]=1 rand2=list(rand2.keys()) mid=np.zeros((h,w),dtype=np.uint8) plain=np.zeros((h,w),dtype=np.uint8) temp1=int(3.99999 *conf_key5*(1 -conf_key5)*1000 )%256 temp2=int(3.99999 *key_d1*(1 -key_d1)*1000 )%256 for x in range(h): for y in range(w): x2=int(x+p2*y)%h y2=int(q2*x+(p2*q2+1 )*y)%w mid[x][y]=ciph[x2][y2] temp=mid[x][y] mid[x][y]=mid[x][y]^rand2[temp2] temp2=temp x1=int(x+p1*y)%h y1=int(q1*x+(p1*q1+1 )*y)%w plain[x1][y1]=mid[x][y]^rand1[temp1] temp1=ciph[x2][y2] return plain def main (): img_path='./Lena.jpg' img=cv2.imread(img_path,-1 ) key=[] conf_key3=0.12345678912340 conf_key4=0.88795676859468 rand1_key=0.72345678912345 rand2_key=0.33798657654353 a=3.99999 conf_key5=0.12345432167893 key_d1=0.54567894324298 key.append(conf_key3) key.append(conf_key4) key.append(rand1_key) key.append(rand2_key) key.append(a) key.append(conf_key5) key.append(key_d1) img=cv2.imread(img_path,-1 ) img_encrypt=encrypt(img_path,key) cv2.imwrite('./Lena_encrypt2.png' ,img_encrypt) encrypt_path='./Lena_encrypt2.png' img_decrypt=decrypt(encrypt_path,key) decrypt_path='./Lena_decrypt2.png' cv2.imwrite(decrypt_path,img_decrypt) wrong_key=list(key) wrong_key[0 ]+=pow(10 ,-10 ) wrong_decrypt=decrypt(encrypt_path,wrong_key) cv2.imwrite('./wrong_decrypt2.png' ,wrong_decrypt) plt.rcParams['font.sans-serif' ] = ['SimHei' ] plt.subplot(221 ) plt.imshow(img,cmap='gray' ) plt.title('原始图像' ) plt.axis('off' ) plt.subplot(222 ) plt.imshow(img_encrypt,cmap='gray' ) plt.title('加密图像\nconf_key3={}' .format(key[0 ])) plt.axis('off' ) plt.subplot(223 ) plt.imshow(wrong_decrypt,cmap='gray' ) plt.title('解密图像\nconf_key3={}' .format(wrong_key[0 ])) plt.axis('off' ) plt.subplot(224 ) plt.imshow(img_decrypt,cmap='gray' ) plt.title('解密图像\nconf_key3={}' .format(key[0 ])) plt.axis('off' ) plt.tight_layout() plt.show() if __name__ == '__main__' : main()
性能评估 注:
性能评估采用lena.tiff 、baboon.tiff 、couple.tiff 、vegatables.tiff 四张图像。
直方图分析
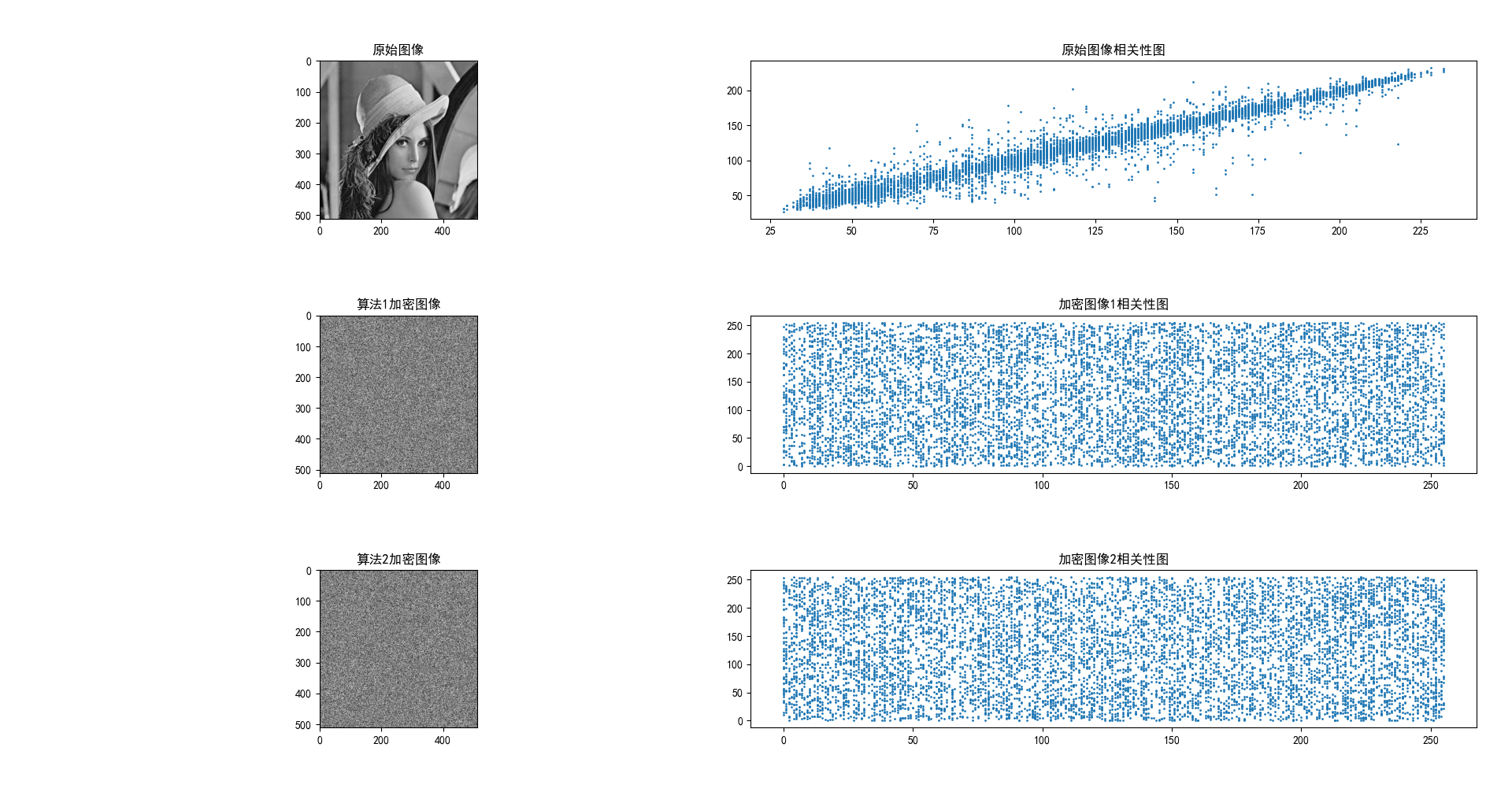
相关性分析 通过分别随机选取3000对相邻像素,根据相关系数的上述定义在水平、垂直和对角方向分别计算原图像和加密图像内的相关系数,实验结果如下:
图像
Horizontal
Vertical
Diagonal
原始图像
0.9737
0.9834
0.9600
算法1加密图像
-0.0184
-0.0277
-0.0116
算法2加密图像
-0.0275
-0.0205
-0.0288
信息熵
信息熵计算
原始图像
算法1加密图像
算法2加密图像
Lena
7.445
7.999
7.998
baboon
7.358
7.999
7.998
couple
6.421
7.997
7.989
vegatables
7.594
7.999
7.998
噪声攻击 对加密图像1分别添加均值为零,方差为0.0001的高斯噪声和5%的校验噪声,然后进行解密,结果如下:
裁剪攻击 从加密图像1中移除(换成0)一块80×80的像素,然后进行解密,结果如下:
重构图像与原始明文图像的PSNR值如下:
计算PSNR
原图-算法1加密图像
原图-算法2加密图像
原图-算法1裁剪重构
原图-算法2裁剪重构
lena
9.228
9.213
22.15
22.32
差分攻击 使用两个测试图像,一个是明文图像Lena,另一个是改变了一位像素的图像,把右下角的108改成了109。c1和c2是两张明文图像相应的加密图像,每幅图像都用相同的密钥加密了几轮。
两幅密文图像的NPCR和UACI计算结果如下
加密轮数(计算NPCR)
算法1
算法2
1
39.7377014%
0.1346588%
2
99.5819092%
29.6928406%
3
99.6105194%
97.6814270%
4
99.6166229%
99.6070862%
加密轮数(计算UACI)
算法1
算法2
1
13.4187616%
0.0474444%
2
33.3877833%
9.9701212%
3
33.4235532%
32.8511960%
4
33.4281203%
33.4886902%
时间分析
加密时间(s)
解密时间(s)
算法1
8.5818
8.3621
算法2
3.5738
3.5558
问题 cat map 长方形图像可以吗???
加密算法2 第二个算法有n轮加密,m轮扩散吗?论文中好像没写,但是不多轮的话,抗差分攻击效果并不好
参考