【论文地址】
基于8阶交替的联合图像压缩与加密
摘要
本文提出了一种基于JPEG标准的联合图像压缩加密方案。我们在JPEG的转换阶段实现了图像加密。代替只使用8*8的DCT变换,我们通过在8*8DCT变换流图中不同阶段的蝴蝶嵌入一个额外的旋转角度$\pi$生成了新的正交变换,然后根据预定义的密钥交替地应用它们进行转换。通过仔细控制嵌入的旋转角度的数量,还可以实现对加密图像的质量控制。通过在熵编码阶段之前进行块排列,进一步增强了加密算法的性能。大量的实验证明了我们的加密方案具有良好的保护和压缩性能。最后,给出了详细的安全性分析,展示了该加密方案对各种密码分析方法的抵抗能力,如蛮力攻击、密钥敏感性分析、替换攻击和统计攻击。
引言
近年来,随着多媒体技术的快速发展,许多功能强大、有趣的新应用被开发出来,人们可以通过不同的社交网络平台来分享存储在移动智能设备上的图片,如Facebook和Instagram。在典型的图像使用中,所有者倾向于将其存储起来以备将来使用,或者通过互联网将其分发给特定的人,而互联网尤其容易被窃听和截取,因此对高效、安全的图像存储和传输有很大的需求。加密是保证图像安全的常用方法之一。
到目前为止,有各种各样的加密技术,比如数据加密标准(DES)和高级加密标准(AES),但它们主要是为文本数据安全而设计的。使用这些传统算法进行图像加密时,由于图像数据量大,计算成本高。
此外,与文本数据不同,图像的信息密度要低得多,许多图像应用程序常常需要实时处理,因此,需要一种计算成本低、加解密速度快的加密策略来保证图像的安全。
在过去,置乱技术被研究者广泛地用于实现图像加密。这些技术包括简单的置换操作和时域或频域的仿射变换操作。然而,随着计算能力的快速提高,破解这种加密方案变得越来越容易。然后,考虑到压缩是我们在互联网上看到的大多数图像必须做的步骤,图像安全研究的重点转移到整合图像压缩过程与加密,以减少图像通信和处理中的加解密时间。这一加密方向最流行的方法是部分加密或选择性加密,它将加密应用于图像压缩系统的最终结果或中间阶段的一部分系数。部分图像加密的主要目的是减少加密数据量,同时获得一定的安全性。
根据加密和压缩过程的处理顺序不同,部分图像加密可分为三类:压缩前、压缩中和压缩后。预压缩是指在压缩之前进行加密,在解密之前进行解压。在[7]中,Tang提出了一种通过使用DES加密直流系数并随机排列交流系数而不是标准之字形扫描顺序来实现部分图像加密的方法。该加密方案的格式符合JPEG,但压缩效率降低了40%左右,因为新的排列打乱了运行长度的概率分布,并使Huffman表的性能低于最优。在压缩类中,图像加解密和压缩解压缩是联合进行的。在[9-11]中,Wu等人在熵编码阶段以秘密顺序交替使用多个Huffman表来实现部分加密。这种加密方案可以在不牺牲压缩性能的情况下实现非常高的视觉退化,但它不符合格式,因为解码器需要解密用于加密的霍夫曼表来做解压缩。后压缩算法在压缩后进行加密,通常是压缩友好的;不需要修改编码器或解码器端的加密和解密。在[12]中,他们提出了一种JPEG图像加密方法,只对霍夫曼编码阶段中用于完全指定非零系数的符号和大小的比特进行加密。该算法视觉退化程度高,格式符合JPEG,但加密参数是静态的,无法进行调优。在[13-16]中,Au-Yeung等人提出在编码过程中通过在转换阶段嵌入加密方案来实现视频的部分加密。由于变换是视频编码器和解码器中必须做的步骤,这种方案的一个明显的优点是它几乎不引入额外的计算。他们通过修改DCT-II的流图结构中的角度值,生成一系列新的正交变换,并根据预定义的密钥交替应用这些新的变换来实现部分视频加密。在[14]中,提出了三种不同的加密算法,并声称Algorithm-3可以在加密能力和编码效率之间取得最佳平衡。
在工作中,我们提出了一种新的联合图像压缩和加密方案,通过在JPEG的转换阶段嵌入加密算法,使图像质量可控。该方案可以在保持JPEG良好压缩性能的同时,达到足够高的安全性,并且格式符合JPEG标准。代替只使用8*8的DCT变换,我们采用在[14]中使用的符号翻转策略来发展新的8阶正交变换,但是我们做符号翻转的蝴蝶与[14]是不同的,导致不同的新的转换集的转换。然后,给出了利用新生成的变换集进行加密的算法。加密和压缩性能通过一些常见的判断标准来评估。并且我们已经证明了我们的新的正交变换比[14]产生的那些有更好的编码效率。通过仔细选择蝴蝶进行角度旋转,可以控制加密图像的视觉质量。此外,为了更好地抵抗直接替换攻击,我们对加密算法进行了修改,增加了块置换操作。最后对所提出的加密方案进行了详细的安全性分析,以展示其对各种攻击的抵抗能力,如蛮力攻击、密钥敏感性分析、替换攻击和统计分析。
新8阶正交变换的生成
在JPEG中,8*8的DCT用来做变换,因为当像素间的相关性很强时,它被证明是压缩能力最好的变换——这在大多数自然图像中都是真实的。在[17]中,以矩阵的形式提出了一个快速DCT-II算法,并通过一个信号流图加以说明。在我们生成新的正交变换的方法中,我们通过引入额外的p旋转角来改进信号流图结构。因此,我们首先介绍了DCT-II的底层快速计算算法,然后解释如何基于它生成新的变换。
DCT-II的一种快速计算算法
这个DCT快速计算算法是基于矩阵分解的,一般情况下,n阶II型DCT矩阵可写成递归形式如下:
$[P_N]$是一个N*N的排列矩阵,将转换后的向量从一个位逆序排列成一个自然的顺序,$[I_{N/2}]$是单位矩阵,$[\overline{I}_{N/2}]$是反对角单位矩阵。$[R_{N/2}]$可以分解成 $(2log_2{N}-3)$个矩阵。
由于在JPEG标准中,只有8阶DCT-II用于转换,所以在这里我们给出了它的流程图如下:
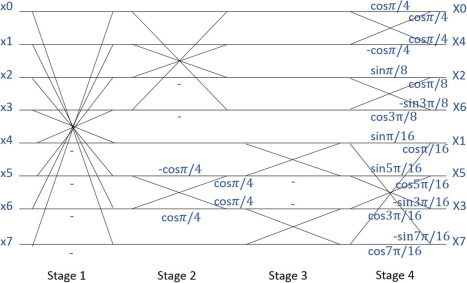
其快速计算公式可描述为:
[M1]的计算相当于流程图中Stage-4的下半部分的蝴蝶
[M2]的计算相当于流程图中Stage-3的下半部分的蝴蝶
[M3]的计算相当于流程图中Stage-2的下半部分的蝴蝶
生成新的正交变换
考虑到加密和压缩性能,新生成的转换的编码效率应该与DCT完全相同,或者只是略有下降。
因此,我们不把角度旋转引入蝴蝶中阶段1和阶段2,因为这会导致变换系数发生较大的变化,最终影响整体编码效率。
在我们的变换生成方法中,使用额外的p的旋转角度,我们生成了两组新的正交变换,TS1和TS2。

