图像压缩加密方面的一些知识
基础知识
图像压缩比?
压缩比是指未压缩图像与压缩图像的比值
joint compression and encryption (JCAE)
DPCM编码简称差值编码
论文
《Joint image compression and encryption using a novel column-wise scanning and optimization algorithm》
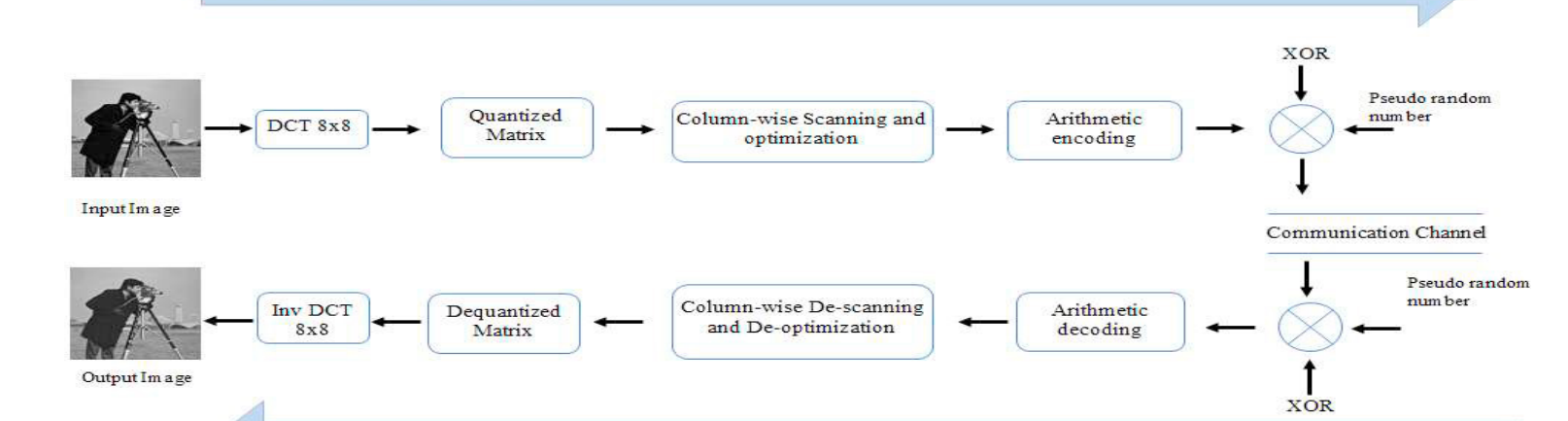
方案:
采用了列扫描优化替换了zigzag锯齿扫描
采用算术编码替换huffman编码
使用128位AES加密 生成伪随机数,然后对算术编码的结果进行异或加密
《Joint compressed sensing and JPEG coding based secure compression scheme in OFDM-PON》
《A Content-Adaptive Joint Image Compression and Encryption Scheme》
加密过程
DCT变换阶段采用不同的正交矩阵 这一步是不影响压缩性能的
量化后 置乱量化块 这一步也不影响压缩性能 并且这个置乱效果和先对8*8图像块置乱再变换是一样的 到此为止图像的统计信息还是没有变化
异或操作改变每个量化块的DC系数
AC系数嵌入Key1
非零交流系数选取256个 然后改变他们的值 嵌入
统计直方图就均匀了?什么道理呢,要做实验去看看
https://www.sciencedirect.com/science/article/pii/S104732031830292X
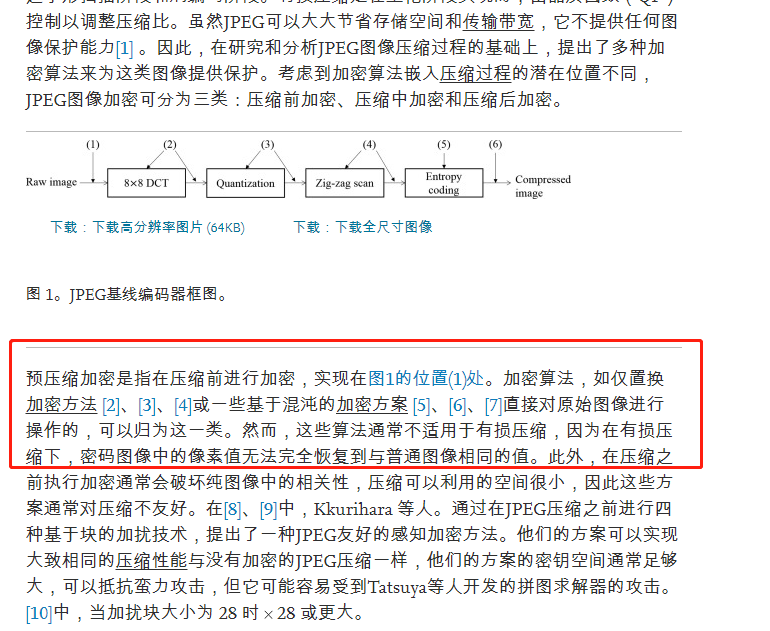
Joint image encryption and compression schemes based on 16 * 16 DCT
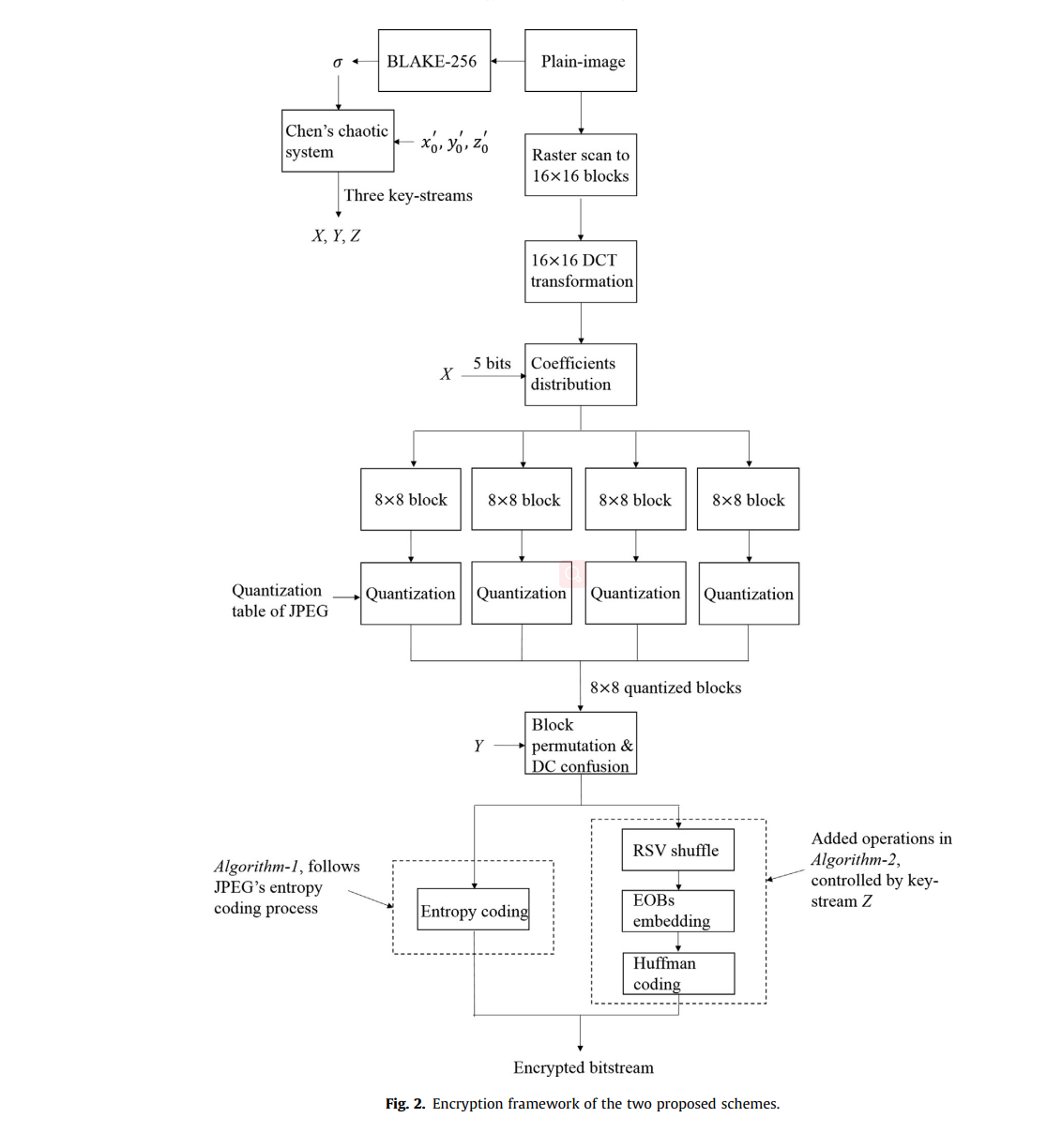
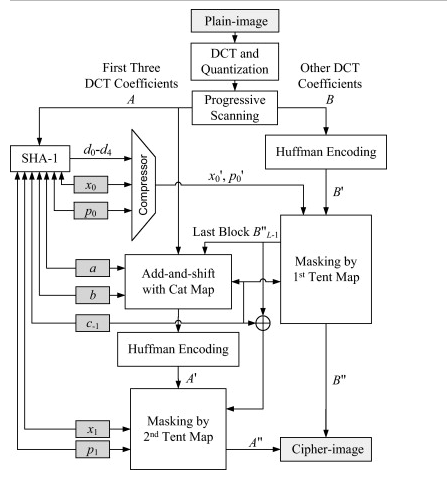
A chaos-based joint image compression and encryption scheme using DCT and SHA-1
总结:
常规的图像加密都是先将图像rgb数据加密后 再进行压缩传输,属于先加密再压缩,而图像压缩就是利用图像像素之间的相关性进行的,图像加密会破坏图像像素之间的相关性,所以加密之后再进行图像压缩,压缩效率会很低,从之前的图像加密结果可以更直观的看出这种差距

一副512*512大小的图像经过加密压缩后得到的大小比之前直接压缩要大很多,几乎没有进行压缩。
先压缩再加密
FF字节后没有补0就是出现波形
思考
加密时直接对图像进行异或加密效果好么?有什么缺点?
答:
图像rgb数据和使用pwlcm产生的混沌序列直接异或,还是可以直观的看出图像的轮廓,可能是因为只进行了扩散 没有置乱操作

加上一个置乱操作 结果就会好很多

只进行置乱,直观上已经看不出什么信息了,但是统计分析不行

不进行像素置乱压缩 和置乱后压缩 压缩效率会降低,探究一下如何不进行置乱在降低像素相关性的同时 尽可能不影响压缩效率,
思考一下dct变换的过程,看看有没有特定的置乱策略 不影响压缩性能

注:before.jpg是不置乱直接进行压缩,after.jpg是rgb三个通道联合置乱后进行压缩,可以看出置乱降低了压缩效率
接下来探究块内置乱,可以列出块内置乱后 压缩效率和压缩质量的关系,压缩质量越大 对压缩效率的影响越大
置乱过程可以考虑解密时像素不恢复到原来的位置 而是
比如 4个像素 a b c d e f g h
混沌系统产生的混沌序列是均匀分布的吗???
答对 测试了lorenz混沌系统产生的混沌序列 分布比较均匀,但是pwlcm混沌系统不是均匀的
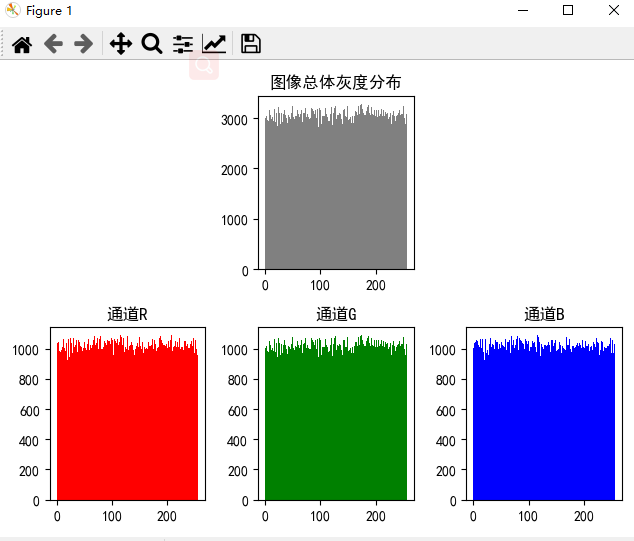
做实验
jpeg c++源码运行并分析
md5加密
考虑不同的dct矩阵 这样不影响压缩又会有加密效果
提出的方案
sha256算法 对不同的明文产生不同的密钥 可以提高加密系统的健壮性
密钥为lorenz混沌系统的3个初始值 x0,y0,z0
sha256产生256bit key
初始化密钥
ck= key中 1的个数
x0_num key中1、3、6位置1的个数
y0_num key中2、4、7位置1的个数
z0_num key中3、5、8位置1的个数
初始化公式
x1=((x0+x0_sum)/(ck+x0+y0+z0))%1
得到三个混沌序列Y Z Q
序列Y 控制DCT变换矩阵的选择
把序列Y的值映射到0-128之间
dct变换阶段采用不同的正交矩阵 这样可以在不影响压缩性能的情况下提高加密能力
使用混沌序列控制选择不同的正交矩阵 这里指的是为每一个8*8块选择一个dct矩阵
块间置乱 采用不同的加密 可以左右互换 上下互换 这样不会改变像素相关性 也就是说不会影响压缩性能但又会提高加密能力
huffman表 置乱 生成新的huffman表
计划
1月19日
看大量论文,总结归纳其中使用的联合压缩加密算法
1月20日
JPEG压缩算法实现以及探究各阶段加密对压缩的性能影响
1月21日
提出算法
1月22日
实现并进行性能评估
1月23日
向老师汇报
1月24日
回家
jpeg压缩的四个阶段
DCT变换 、量化、锯齿扫描 熵编码
理论上 Dct变换不会影响压缩性能
量化块置乱也不会

