DCT离散余弦变换

引言

DCT变换的全称是离散余弦变换(Discrete Cosine Transform)，主要用于数据或图像的压缩，能够将空域的信号转换到频域上，具有良好的去相关性的性能。

DCT变换本身是无损的，但是在图像编码等领域给接下来的量化、哈弗曼编码等创造了很好的条件，同时，由于DCT变换是对称的，所以，我们可以在量化编码后利用DCT逆变换，在接收端恢复原始的图像信息。DCT变换在当前的图像分析以及压缩领域有着极为广大的用途，我们常见的JPEG静态图像编码以及MJPEG、MPEG动态编码等标准中都使用了DCT变换。

一维DCT变换

一维DCT变换是二维DCT变换的基础，所以我们先来讨论一下一维DCT变换。一维DCT变换共有8种形式，其中最常用的是第二种形式，由于其运算简单、适用范围广，我们在这里只讨论这种形式，其表达式如下：

$F(u)=c(u)\sum^{N-1}_{i=0}f(i){cos[\frac{(i+0.5)\pi}{N}u]}$ $c(u)=\left\{ \begin{array}{l} \sqrt{\frac{1}{N}},u=0\\ \sqrt{\frac{2}{N}},u\neq0 \end{array} \right .$

其中，f(i)为原始的信号，F(u)是DCT变换后的系数，N为原始信号的点数，c(u)可以认为是一个补偿系数，可以使DCT变换矩阵为正交矩阵。

二维DCT变换

二维DCT变换其实是在一维DCT变换的基础上再做了一次DCT变换，其公式如下：

$F(u,v)=c(u)c(v)\sum^{N-1}_{i=0}{\sum^{N-1}_{j=0}{f(i,j)cos[\frac{(i+0.5)\pi}{N}u]cos[\frac{(j+0.5)\pi}{N}v]}}$ $c(u)=\left\{ \begin{array}{l} \sqrt{\frac{1}{N}},u=0\\ \sqrt{\frac{2}{N}},u\neq0 \end{array} \right .$

由公式我们可以看出，上面只讨论了二维图像数据为方阵的情况，在实际应用中，如果不是方阵的数据，一般都是补齐之后再做变换的，重构之后可以去掉补齐的部分，得到原始的图像信息，这个尝试一下，应该比较容易理解。

另外，由于DCT变换高度的对称性，在使用python进行相关的运算时，可以使用更简单的矩阵处理方式：

$F=AfA^T$ $A(i,j)=c(i)cos[\frac{(j+0.5)\pi}{N}i]$

二维DCT逆变换

在图像的接收端，根据DCT变化的可逆性，我们可以通过DCT逆变换恢复出原始的图像信息，公式如下：

$f(i,j)=\sum^{N-1}_{u=0}{\sum^N-1}_{v=0}{c(u)c(v)F(u,v)cos[\frac{(i+0.5)\pi}{N}u]cos[\frac{(j+0.5)\pi}{N}v]}$ $c(u)=\left\{ \begin{array}{l} \sqrt{\frac{1}{N}},u=0\\ \sqrt{\frac{2}{N}},u\neq0 \end{array} \right .$

同样的道理，我们利用之前的矩阵运算公式可以推导出DCT逆变换相应的矩阵形式：

$f=A^TFA$ $A(i,j)=c(i)cos[\frac{(j+0.5)\pi}{N}i]$

仿真实验

接下来使用python对变换过程进行仿真实验：

实验代码

import numpy as np
import cv2

#传入要计算的方阵
def cal_dct(X):
	N=X.shape[0]
	A=np.zeros((N,N))
	# print(X)
	for i in range(N):
		for j in range(N):
			if i == 0:
				a=np.sqrt(1/N)
			else:
				a=np.sqrt(2/N)
			A[i,j]=a*np.cos(np.pi*(j+0.5)*i/N)
	#DCT变换
	#dot矩阵乘法，*号是对应元素相乘
	Y=A.dot(X).dot(A.T)
	return Y

def cal_idct(X):
	N=X.shape[0]
	A=np.zeros((N,N))
	for i in range(N):
		for j in range(N):
			if i == 0:
				a=np.sqrt(1/N)
			else:
				a=np.sqrt(2/N)
			A[i,j]=a*np.cos(np.pi*(j+0.5)*i/N)
	#DCT变换
	#dot矩阵乘法，*号是对应元素相乘
	Y=(A.T).dot(X).dot(A)
	return Y


def main():
	#指定二维方阵
	X=np.array([[42,66,68,66],[92,4,76,17],[79,85,74,71],[96,93,39,3]],dtype=np.float64)
	#DCT变换
	Y=cal_dct(X)
	print('dct公式计算结果如下:')
	print(Y)
	#使用opencv库中的dct函数计算
	YY=cv2.dct(X)
	print('使用opencv库中的dct函数计算结果如下:')
	print(YY)
	
	#DCT逆变换
	X=cal_idct(Y)
	print('idct公式计算结果如下:')
	print(X)

	#使用opencv库中的idct函数计算
	XX=cv2.idct(YY)
	print('使用opencv库中的idct函数计算结果如下:')
	print(XX)

if __name__ =='__main__':
	main()

实验结果

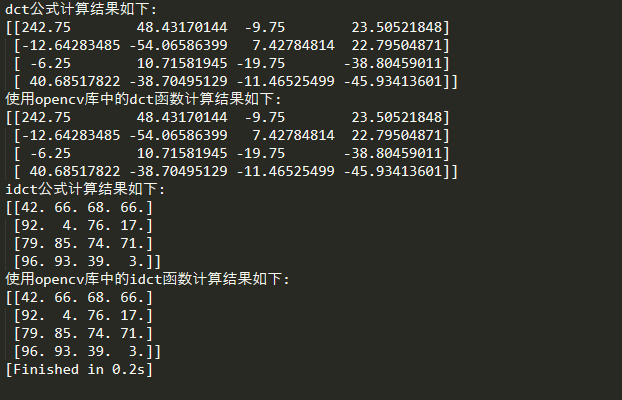
由实验结果可以看出，我们采用的公式的方法和python openCV模块自带的dct函数结果是一致的，验证了我们方法的正确性。

如果原始信号是图像等相关性较大的数据的时候，我们可以发现在变换之后，系数较大的集中在左上角，而右下角的几乎都是0，其中左上角的是低频分量，右下角的是高频分量，低频系数体现的是图像中目标的轮廓和灰度分布特性，高频系数体现的是目标形状的细节信息。DCT变换后，能量主要集中在低频分量处，这也是DCT变换去相关性的一个体现。之后在量化和编码阶段，我们可以用“Z”字形编码，这样就可以得到大量的连续的0，这大大简化了编码的过程。

另外我们也可以看到逆变换后无损的恢复了原始信息，所以证明了方法的正确性。但是在实际过程中，需要量化编码或者直接舍弃高频分量等处理，所以会出现一定程度的误差，这个是不可避免的。

CTF of Z2BNS

DCT离散余弦变换

引言

一维DCT变换

二维DCT变换

二维DCT逆变换

仿真实验

参考